Graded Intervention Time Series: Introduction#
Graded Intervention Time Series extends classical interrupted time series analysis to handle graded interventions - policies or treatments with varying intensity over time, rather than simple on/off changes. Traditional ITS methods model binary interventions (e.g., “policy enacted” vs “no policy”). This method (technically called Transfer Function Interrupted Time Series or TF-ITS in the literature [Box and Tiao, 1975], with extensions to multiple time series by [Abraham, 1980]) handles more realistic scenarios where:
Intervention intensity varies continuously (e.g., advertising spend $0 - 100k, communication frequency 0-10 messages/week)
Effects persist over time - past interventions continue to influence outcomes (behavioral habits change gradually, messages have carryover effects)
Effects may saturate (optional) - diminishing returns as exposure increases (10th message less impactful than the 1st)
For a good introductory overview of transfer function models and intervention analysis, see [Helfenstein, 1991].
Key Components#
Transfer functions: Transform the raw intervention variable to capture its dynamic relationship with the outcome. In the media mix modeling literature, two common transfer functions are:
Adstock (carryover) transforms: Model how effects persist over time using geometric decay with configurable half-life
Saturation transforms (optional): Model diminishing returns using Hill, logistic, or Michaelis-Menten functions when appropriate
CausalPy leverages transformation functions from
pymc-marketing[PyMC Labs, 2025] to model both temporal dynamics (how effects persist over time) and intensity dynamics (how effects change with intervention strength).Baseline controls: Include confounders and natural trends in the regression
Counterfactual analysis: Estimate causal effects by zeroing or scaling interventions
Error model for autocorrelation: Time series data typically exhibits autocorrelation (temporal dependence in residuals), which requires special handling for valid inference. This can be addressed through multiple approaches including HAC (Newey-West) standard errors or ARIMAX error models (see detailed discussion below).
Transfer functions can be as simple as a distributed lag (adstock only) or can combine multiple transformations (e.g., saturation followed by adstock). The key is to match the functional form to the expected dynamics of the intervention.
When to Use Graded Intervention Time Series#
Use this method when you have:
✅ Time series data from a single unit (region, market, organization)
✅ Graded intervention with varying intensity over time
✅ Reason to expect carryover effects (persistence over time), and optionally saturation (diminishing returns)
✅ Baseline controls available for confounders
Note
This notebook demonstrates the single channel (single time series) case. The transfer function intervention analysis framework extends naturally to multiple time series [Abraham, 1980], but this extension is not yet implemented in CausalPy.
Compare to related methods:
Classic Interrupted Time Series: Binary on/off intervention (no dose-response modeling)
Synthetic Control: Multiple control units available for comparison
Difference in Differences: Panel data with treatment/control groups
The Autocorrelation Challenge#
Introduction: Understanding the Problem#
Autocorrelation occurs when observations in a time series are correlated with their own past values. In causal inference with time series data, this creates a fundamental challenge:
What is autocorrelation?
Today’s outcome is influenced by yesterday’s (and last week’s, and last month’s…)
This happens through multiple mechanisms:
Persistent unobserved factors: Weather patterns, economic conditions, social trends
Behavioral inertia: Habits and routines change slowly
Institutional dynamics: Organizational processes have memory
Measurement systems: Data collection schedules create patterns
Why is this a problem for causal inference?
Standard regression assumes independent errors — that the unexplained variation at time \(t\) is unrelated to time \(t-1\). When this assumption fails (as it almost always does in time series):
✅ Coefficient estimates remain unbiased: still correct on average
❌ Standard errors are WRONG: typically too small, making confidence intervals too narrow
❌ Hypothesis tests are invalid: false positives, misleading p-values
This means you might conclude an intervention “works” when it actually doesn’t, or claim high precision when you’re actually quite uncertain!
How to handle autocorrelation:
There are several approaches to addressing autocorrelation in time series causal inference:
HAC (Newey-West) standard errors: Correct standard errors without modeling autocorrelation structure
ARIMAX models: Explicitly model AR/MA error structure
GLSAR: Generalized least squares with autoregressive errors
Bayesian time series models: Full posterior inference with temporal dependencies
Bootstrap methods: Resample with preserved temporal structure
This implementation provides both HAC and ARIMAX approaches, each with distinct advantages for different use cases.
Approach 1: HAC Standard Errors (Default)#
Time series data typically exhibits autocorrelation (past values influence current values) and heteroskedasticity (variance changes over time). When these violations occur, OLS coefficient estimates remain unbiased, but standard errors are incorrect—typically too small, leading to overconfident inference with narrow confidence intervals and artificially low p-values.
HAC (Heteroskedasticity and Autocorrelation Consistent) standard errors — also known as Newey-West standard errors [Newey and West, 1987] — provide robust inference by correcting standard errors for these violations without requiring specification of the autocorrelation structure.
Why use HAC?
Simplicity: No need to specify autocorrelation structure (order of AR/MA terms)
Robustness: Works with any autocorrelation pattern (not just AR or MA)
Computational efficiency: Fast OLS with corrected standard errors
Valid inference: Causal estimates remain unbiased and confidence intervals account for autocorrelation
Proven reliability: Well-established method with strong theoretical properties
Key parameter: CausalPy uses the Newey-West rule of thumb for hac_maxlags: floor(4*(n/100)^(2/9)). For our 156-week dataset, this gives hac_maxlags=4, accounting for up to 4 weeks of residual correlation.
Tradeoff: HAC standard errors are wider (more conservative) than naive OLS, but they provide trustworthy inference even when residuals show complex autocorrelation patterns.
This notebook demonstrates HAC inference in the main analysis sections, showing how it compares to naive OLS and why it matters for valid causal inference.
Approach 2: ARIMAX Models#
ARIMAX (ARIMA with eXogenous variables) explicitly models the autocorrelation structure of residuals using ARIMA(p,d,q) processes, following the classical Box & Tiao (1975) intervention analysis framework [Box and Tiao, 1975].
Advantages:
Efficiency: Smaller standard errors when ARIMA structure is correctly specified
Classical methodology: Follows the original intervention analysis approach
Explicit error modeling: Can characterize and forecast residual dynamics
Tradeoffs:
Requires specification: Must choose p, d, q orders (typically via ACF/PACF plots)
Misspecification risk: Wrong orders can lead to biased or inefficient inference
Less robust: More sensitive to outliers and structural breaks
A later section of this notebook demonstrates ARIMAX as an alternative error model, comparing it to HAC and providing guidance on when to use each approach.
Notebook Overview#
This notebook demonstrates Graded Intervention Time Series (Transfer Function ITS) analysis using a simulated water consumption dataset. We’ll walk through data simulation, model fitting with transform parameter estimation, diagnostic checks, counterfactual analysis, and a comparison of different approaches to handling autocorrelation in time series data (HAC vs ARIMAX error models).
Implementation notes
This notebook demonstrates multiple approaches to Transfer Function ITS:
OLS regression with HAC standard errors (fast, robust inference)
OLS with ARIMAX error models (explicit autocorrelation modeling)
Automated transform parameter estimation (grid search and continuous optimization)
Bayesian inference with PyMC (full posterior uncertainty quantification)
Example Scenario: Water Restrictions Policy#
A regional water authority in a dry climate implements a drought-responsive communications policy. Communication intensity (0-10 scale) activates during sustained drought conditions (low 6-week cumulative rainfall and high temperature), with intensity varying based on severity. Communications are zero most of the time, activating only during drought periods.
Why this example demonstrates TF-ITS strengths:
Graded intervention: Communication intensity varies from 0-10 based on drought severity, not binary on/off
Realistic on/off activation: Policy activates only during drought (sparse, realistic)
Adstock: Short carryover effect (~1.5 week half-life) - behavior reverts quickly when messaging stops
Confounders: Temperature and rainfall directly affect water consumption and must be controlled
Note: Water consumption exhibits shorter persistence than interventions like advertising or habit-forming behaviors, since consumption is largely need-driven and reverts quickly when environmental conditions (rainfall, temperature) change.
Transfer function specification for this example:
In this notebook, we model the intervention using only an adstock (carryover) transform without saturation. This is appropriate for water conservation communications because:
The main dynamic is temporal persistence of behavior change (carryover from past messages)
There’s no strong theoretical reason to expect diminishing returns in this range of intensity (0-10 messages)
Simpler models with fewer parameters often provide better parameter recovery and more reliable inference
However, CausalPy’s implementation supports flexible transform configurations to match your causal assumptions:
Adstock only (this notebook’s approach) - captures carryover effects
Saturation only - captures diminishing returns without carryover
Both transforms - combines saturation and adstock when both dynamics are expected (e.g., high-frequency advertising with both diminishing returns and carryover)
The choice should be guided by domain knowledge and the expected dynamics of your intervention.
While we use water policy, this method applies to any domain with graded interventions and carryover effects:
Public health campaigns (vaccination messaging, smoking cessation)
Marketing mix modeling (advertising spend, promotions)
Environmental policy (emissions reduction programs)
Traffic management (congestion pricing communications)
Education interventions (remediation program intensity)
We’ll simulate weekly water consumption data for a catchment area in a dry climate over 3 years with:
Baseline drivers: temperature (seasonal) and rainfall (very low, with drought periods)
Responsive policy: public communications intensity that activates only during sustained drought
Autocorrelated errors: AR(2) process to simulate realistic residual autocorrelation (this demonstrates why HAC standard errors are crucial!)
Seasonal heteroskedasticity: Error variance increases during summer months (higher volatility)
Key features:
Rainfall ranges 0-16 mm/week with extended zero-rainfall periods in summer
Communication intensity activates during drought (6-week rainfall < 25mm and temp > 25°C)
Policy responds to 6-week cumulative rainfall deficit and current temperature
When active, intensity varies 5-10 based on drought severity (not binary)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import causalpy as cp
# Set random seed for reproducibility
np.random.seed(42)
%config InlineBackend.figure_format = 'retina'
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
/Users/benjamv/mambaforge/envs/CausalPy/lib/python3.13/site-packages/pymc_extras/model/marginal/graph_analysis.py:10: FutureWarning: `pytensor.graph.basic.io_toposort` was moved to `pytensor.graph.traversal.io_toposort`. Calling it from the old location will fail in a future release.
from pytensor.graph.basic import io_toposort
# Generate 156 weeks (3 years) of data
n_weeks = 156
dates = pd.date_range("2022-01-01", periods=n_weeks, freq="W-MON")
t = np.arange(n_weeks)
# Temperature (°C): seasonal pattern with summer peaks (southern hemisphere)
# Peak in Jan (week ~0) and Dec (week ~52), low in July (week ~26)
temperature = 25 + 10 * np.sin(2 * np.pi * t / 52) + np.random.normal(0, 2, n_weeks)
# Rainfall (mm/week): inverse seasonal pattern - very low in summer, moderate in winter
# Drier climate with extended periods of zero rainfall creating drought conditions
rainfall = 8 - 8 * np.sin(2 * np.pi * t / 52) + np.random.normal(0, 3, n_weeks)
rainfall = np.maximum(rainfall, 0) # Censor at zero (no negative rainfall)
# Communication intensity (scale 0-10): On/off activation during drought with graded intensity
# Policy responds to cumulative rainfall deficit over past 6 weeks
comm_intensity = np.zeros(n_weeks)
# Calculate 6-week rolling sum of rainfall (measure of drought severity)
window_size = 6
for i in range(n_weeks):
start_idx = max(0, i - window_size + 1)
rainfall_6wk = rainfall[start_idx : i + 1].sum()
# Trigger communications during sustained drought conditions
# Expected 6-week rainfall in normal conditions: ~48mm (8mm/week avg)
# Drought threshold: < 25mm over 6 weeks (< 4.2mm/week average)
if rainfall_6wk < 25 and temperature[i] > 25:
# Ramp up intensity based on drought severity
drought_severity = (25 - rainfall_6wk) / 25 # 0 to 1
heat_factor = (temperature[i] - 25) / 10 # 0 to 1
intensity_raw = 5 + 5 * (drought_severity + heat_factor) / 2
comm_intensity[i] = np.clip(intensity_raw, 0, 10)
# Otherwise, communications stay at zero (no routine messaging)
# Baseline water consumption: depends on temperature and rainfall
# Higher temp → more water use, higher rainfall → less water use
baseline = (
4000 # Base consumption
+ 80 * temperature # Temperature effect (~80 ML per degree)
- 20 * rainfall # Rainfall effect (~20 ML per mm)
+ 5.0 * t # Slight upward trend (population growth)
)
# Apply "true" transform to generate the data using pure numpy
# (Note: for data generation, we use numpy. For model fitting, we use CausalPy's transforms)
# Adstock: geometric with half-life of 1.5 weeks
# Short carryover effect - behavior reverts quickly when messaging stops
# (More realistic for water consumption than longer persistence)
half_life = 1.5
alpha = np.power(0.5, 1 / half_life) # decay rate
l_max = 8 # Shorter window since effect decays quickly
# Apply geometric adstock convolution directly to raw communication intensity
comm_transformed = np.zeros_like(comm_intensity)
adstock_weights = np.power(alpha, np.arange(l_max + 1))
adstock_weights = adstock_weights / adstock_weights.sum() # normalize
for t_idx in range(n_weeks):
for lag in range(min(l_max + 1, t_idx + 1)):
comm_transformed[t_idx] += adstock_weights[lag] * comm_intensity[t_idx - lag]
# Generate water consumption with autocorrelated errors (realistic time series)
# Negative coefficient: higher communication intensity → lower water consumption
theta_true = (
-50
) # Treatment coefficient (ML reduction per unit of transformed communication)
# Create AR(2) autocorrelated errors to simulate realistic residual structure
# Even with correct model specification (right variables, right transforms),
# real data has unmodeled factors with temporal persistence:
# - Unmeasured weather patterns (humidity, wind, soil moisture)
# - Social contagion (neighbors influencing each other's conservation behavior)
# - Measurement error with persistence (meter reading schedules)
# - Institutional factors (maintenance schedules, local events)
# This autocorrelation is EXACTLY why we need HAC standard errors!
rho1 = 0.5 # AR(1) coefficient
rho2 = 0.2 # AR(2) coefficient
base_error_sd = 100 # Base standard deviation of innovation
# Add seasonal heteroskedasticity: higher variance in summer (when temperature is high)
# Error SD scales with temperature (normalized to 0-1 range)
temp_normalized = (temperature - temperature.min()) / (
temperature.max() - temperature.min()
)
seasonal_scale = 1 + 0.5 * temp_normalized # SD ranges from 1x to 1.5x base
error_sd_t = base_error_sd * seasonal_scale
# Generate stationary AR(2) process: epsilon_t = rho1 * epsilon_{t-1} + rho2 * epsilon_{t-2} + nu_t
errors = np.zeros(n_weeks)
# Stationary initialization (first two values from unconditional distribution)
var_epsilon = base_error_sd**2 * (1 - rho2) / ((1 + rho2) * ((1 - rho2) ** 2 - rho1**2))
errors[0] = np.random.normal(0, np.sqrt(var_epsilon))
errors[1] = np.random.normal(0, np.sqrt(var_epsilon))
for t_idx in range(2, n_weeks):
errors[t_idx] = (
rho1 * errors[t_idx - 1]
+ rho2 * errors[t_idx - 2]
+ np.random.normal(0, error_sd_t[t_idx])
)
water_consumption = baseline + theta_true * comm_transformed + errors
# Create DataFrame
df = pd.DataFrame(
{
"date": dates,
"t": t,
"water_consumption": water_consumption,
"temperature": temperature,
"rainfall": rainfall,
"comm_intensity": comm_intensity,
}
)
df = df.set_index("date")
Show code cell source
print(df.head(10))
print(f"\nData shape: {df.shape}")
print(
f"Water consumption range: [{df['water_consumption'].min():.0f}, {df['water_consumption'].max():.0f}] ML/week"
)
print(
f"Temperature range: [{df['temperature'].min():.1f}, {df['temperature'].max():.1f}] °C"
)
print(
f"Rainfall range: [{df['rainfall'].min():.1f}, {df['rainfall'].max():.1f}] mm/week"
)
print(f" Number of zero-rainfall weeks: {(df['rainfall'] == 0).sum()}")
print(f" Number of weeks with rainfall < 2mm: {(df['rainfall'] < 2).sum()}")
print(
f"Communication intensity range: [{df['comm_intensity'].min():.1f}, {df['comm_intensity'].max():.1f}]"
)
print(
f" Number of weeks with active communications (>0): {(df['comm_intensity'] > 0).sum()}"
)
t water_consumption temperature rainfall comm_intensity
date
2022-01-03 0 5795.367711 25.993428 13.597324 6.388625
2022-01-10 1 5837.000864 25.928838 8.457205 5.526757
2022-01-17 2 6276.184534 28.688534 2.511564 5.965524
2022-01-24 3 6405.256715 31.592109 7.132822 0.000000
2022-01-31 4 6451.142513 29.178925 1.358170 0.000000
2022-02-07 5 6363.829835 30.212374 5.816736 0.000000
2022-02-14 6 6790.464732 34.789652 6.170805 0.000000
2022-02-21 7 6662.707405 34.019977 0.000000 7.455985
2022-02-28 8 6381.078759 32.290890 4.306257 6.844243
2022-03-07 9 6639.278815 34.939680 2.154695 8.004254
Data shape: (156, 5)
Water consumption range: [4657, 7694] ML/week
Temperature range: [11.4, 38.8] °C
Rainfall range: [0.0, 21.2] mm/week
Number of zero-rainfall weeks: 17
Number of weeks with rainfall < 2mm: 34
Communication intensity range: [0.0, 9.9]
Number of weeks with active communications (>0): 53
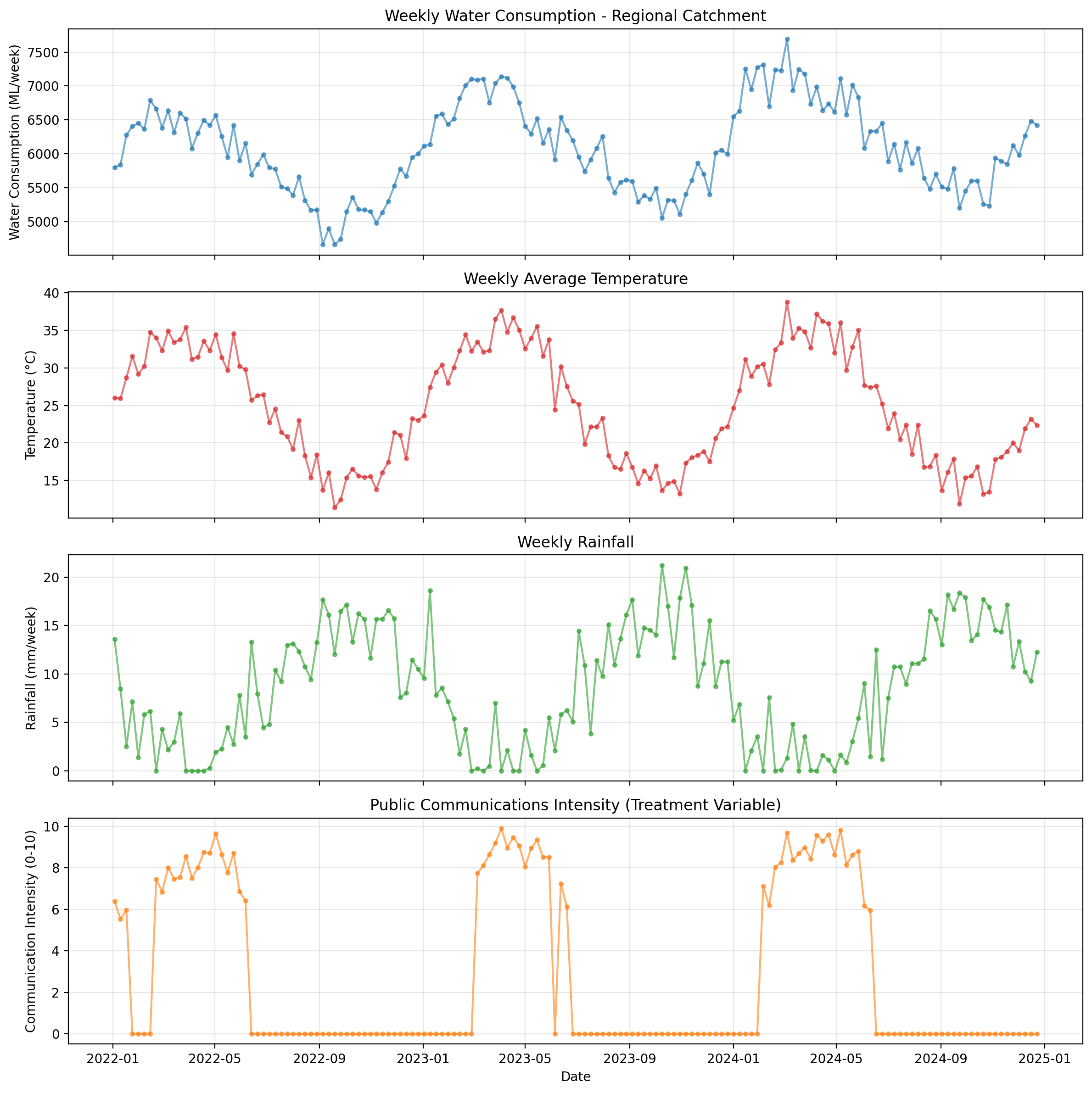
Let’s look at the water consumption and communication intensity time series. Notice:
Very dry climate with extended zero-rainfall periods in summer
Communications activate during drought periods (mostly zero, then 5-10 when conditions met)
Policy responds to cumulative rainfall deficit over the past 6 weeks and current temperature
Realistic on/off pattern with graded intensity when active
Show code cell source
fig, axes = plt.subplots(4, 1, figsize=(12, 12), sharex=True)
# Water consumption
axes[0].plot(df.index, df["water_consumption"], "o-", alpha=0.6, markersize=3)
axes[0].set_ylabel("Water Consumption (ML/week)")
axes[0].set_title("Weekly Water Consumption - Regional Catchment")
axes[0].grid(True, alpha=0.3)
# Temperature
axes[1].plot(df.index, df["temperature"], "o-", alpha=0.6, markersize=3, color="C3")
axes[1].set_ylabel("Temperature (°C)")
axes[1].set_title("Weekly Average Temperature")
axes[1].grid(True, alpha=0.3)
# Rainfall
axes[2].plot(df.index, df["rainfall"], "o-", alpha=0.6, markersize=3, color="C2")
axes[2].set_ylabel("Rainfall (mm/week)")
axes[2].set_title("Weekly Rainfall")
axes[2].grid(True, alpha=0.3)
# Communication intensity
axes[3].plot(df.index, df["comm_intensity"], "o-", alpha=0.6, markersize=3, color="C1")
axes[3].set_ylabel("Communication Intensity (0-10)")
axes[3].set_title("Public Communications Intensity (Treatment Variable)")
axes[3].set_xlabel("Date")
axes[3].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# Show correlation between variables
print("\nKey patterns in the data:")
print(
"- Very dry climate: 0-16mm/week rainfall, with extended zero-rainfall periods in summer"
)
print("- Communication intensity mostly zero, activates during drought")
print("- Activates when 6-week rainfall < 25mm and temperature > 25°C")
print("- When active, intensity varies 5-10 based on severity (graded, not binary)")
print("- Realistic on/off pattern with sparse activation periods")
Key patterns in the data:
- Very dry climate: 0-16mm/week rainfall, with extended zero-rainfall periods in summer
- Communication intensity mostly zero, activates during drought
- Activates when 6-week rainfall < 25mm and temperature > 25°C
- When active, intensity varies 5-10 based on severity (graded, not binary)
- Realistic on/off pattern with sparse activation periods
Modelling with HAC#
Fitting a transfer function model involves finding both the optimal transform parameters and the regression coefficients. This is accomplished through a nested optimization procedure. In the outer loop, the algorithm searches for the best adstock parameter (half-life)—either by exhaustively evaluating all values on a discrete grid, or by using continuous optimization to search more efficiently through the parameter space. For each candidate adstock parameter, the inner loop applies this transformation to the raw treatment variable and fits a regression model (OLS or ARIMAX) to the data. The root mean squared error (RMSE) of each fitted model is computed, and the parameter value that minimizes this error is selected.
This nested approach is computationally tractable because ordinary least squares has a closed-form solution based on matrix operations, making each individual model fit very fast. When using grid search with 30 values for the adstock half-life parameter, the algorithm evaluates 30 model fits, which typically completes in under a second. Continuous optimization via gradient-based methods can be even faster, though it may settle on local optima rather than finding the global best. For models with ARIMAX error structures, each fit requires numerical optimization and takes longer, but the overall approach remains the same.
Fit Model#
Let’s fit a model using grid search to estimate the adstock half-life parameter. We use a fine grid (30 points) to achieve good parameter recovery.
model_estimated = cp.skl_models.TransferFunctionOLS(
saturation_type=None, # No saturation - adstock only
adstock_grid={
"half_life": np.linspace(0.5, 3.0, 30), # Finer grid: 30 points (was 10)
"l_max": [8], # Fixed
"normalize": [True], # Fixed
},
estimation_method="grid", # or "optimize"
error_model="hac",
)
result_estimated = cp.GradedInterventionTimeSeries(
data=df,
y_column="water_consumption",
treatment_names=["comm_intensity"],
base_formula="1 + t + temperature + rainfall",
model=model_estimated,
)
print("Parameter estimation complete!")
print(f"Best RMSE: {result_estimated.transform_estimation_results['best_score']:.2f}")
print(f"Model R-squared: {result_estimated.score:.4f}")
print("\nEstimated parameters:")
print(result_estimated.transform_estimation_results["best_params"])
Parameter estimation complete!
Best RMSE: 132.21
Model R-squared: 0.9584
Estimated parameters:
{'half_life': np.float64(3.0), 'l_max': 8, 'normalize': True}
Visualize Estimated vs True Transform Parameters#
Since we know the true parameters used to generate the data, we can compare the estimated transform to the true transform. This helps us assess parameter recovery - how well the estimation procedure identifies the true data-generating process.
We’ll visualize the adstock weights: How effects carry over across weeks
# Create true transform object (parameters used for data generation)
true_adstock = cp.GeometricAdstock(half_life=1.5, l_max=8, normalize=True)
# Plot estimated transform with comparison to true transform
fig, ax = result_estimated.plot_transforms(
true_saturation=None, true_adstock=true_adstock, x_range=(0, 10)
)
plt.show()
# Parameter Recovery Assessment
true_adstock_params = true_adstock.get_params()
est_adstock_params = result_estimated.treatments[0].adstock.get_params()
print("\nParameter Recovery Assessment:")
print(
f"Adstock half_life - True: {true_adstock_params['half_life']:.2f}, Estimated: {est_adstock_params['half_life']:.2f}, Error: {abs(est_adstock_params['half_life'] - true_adstock_params['half_life']):.2f} weeks"
)
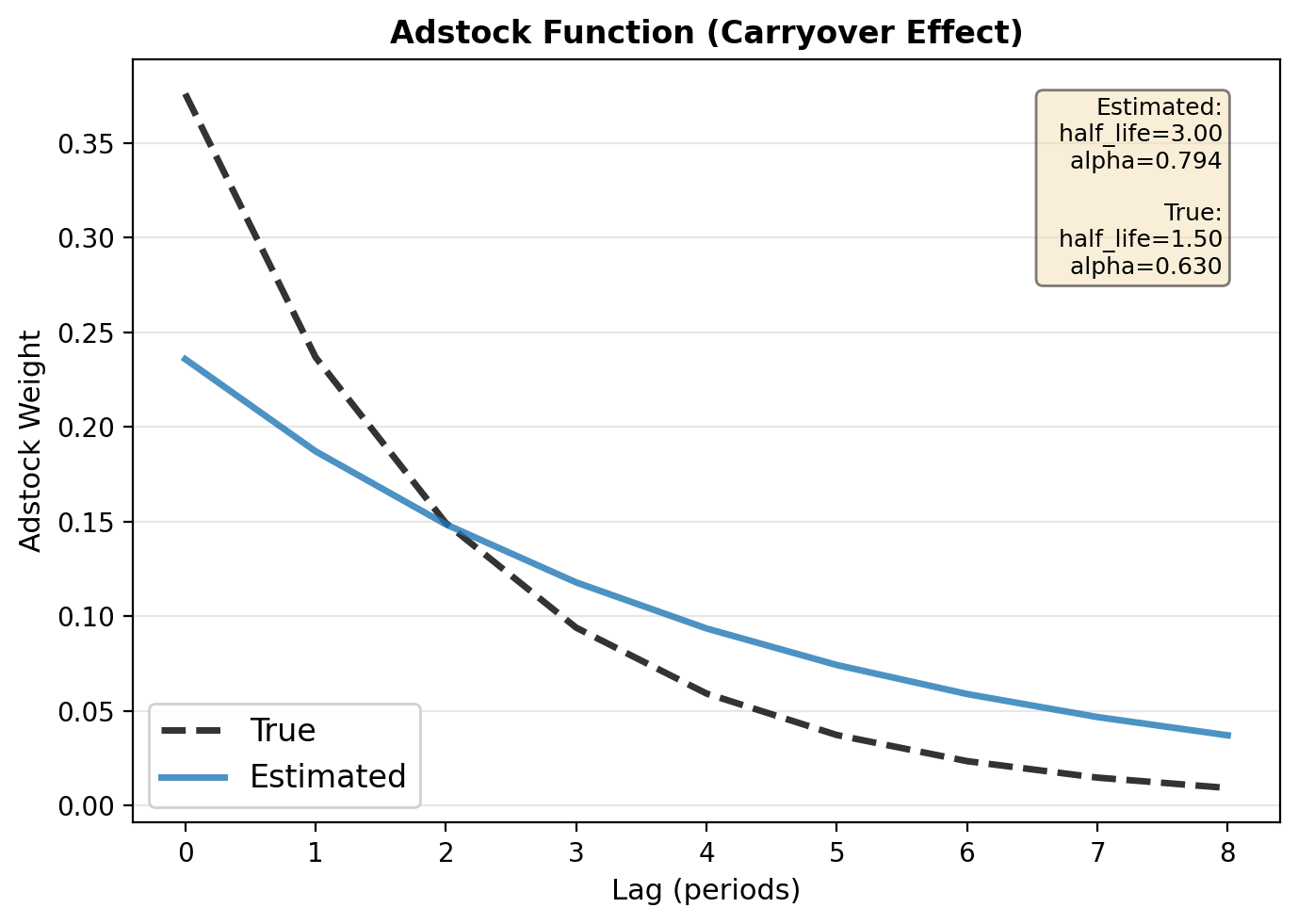
Parameter Recovery Assessment:
Adstock half_life - True: 1.50, Estimated: 3.00, Error: 1.50 weeks
Interpretation:
Adstock weights: Shows how a communication “impulse” at week 0 affects water consumption over the following weeks. With the true half-life of 1.5 weeks, about 50% of the effect persists after 1.5 weeks. The bars show the relative contribution of each lag.
Parameter recovery: In this simulated example with known ground truth, we can assess how well the estimation recovered the true adstock parameter (half_life = 1.5 weeks). Good recovery suggests the model specification is appropriate and the data is informative.
In real applications (without ground truth), you would:
Use domain knowledge to set reasonable parameter grids/bounds for adstock half-life
Compare estimated decay patterns to expert expectations about effect persistence
Check sensitivity of results to different half-life ranges
Model Summary#
View the fitted model coefficients and their HAC standard errors (robust to autocorrelation and heteroskedasticity):
# Display model summary
result_estimated.summary(round_to=2)
================================================================================
Graded Intervention Time Series Results
================================================================================
Outcome variable: water_consumption
Number of observations: 156
R-squared: 0.96
Error model: HAC
HAC max lags: 4 (robust SEs accounting for 4 periods of autocorrelation)
--------------------------------------------------------------------------------
Baseline coefficients:
Intercept : 3809 (SE: 92)
t : 4.8 (SE: 0.33)
temperature : 93 (SE: 3.3)
rainfall : -24 (SE: 2.9)
--------------------------------------------------------------------------------
Treatment coefficients:
comm_intensity : -70 (SE: 7.5)
================================================================================
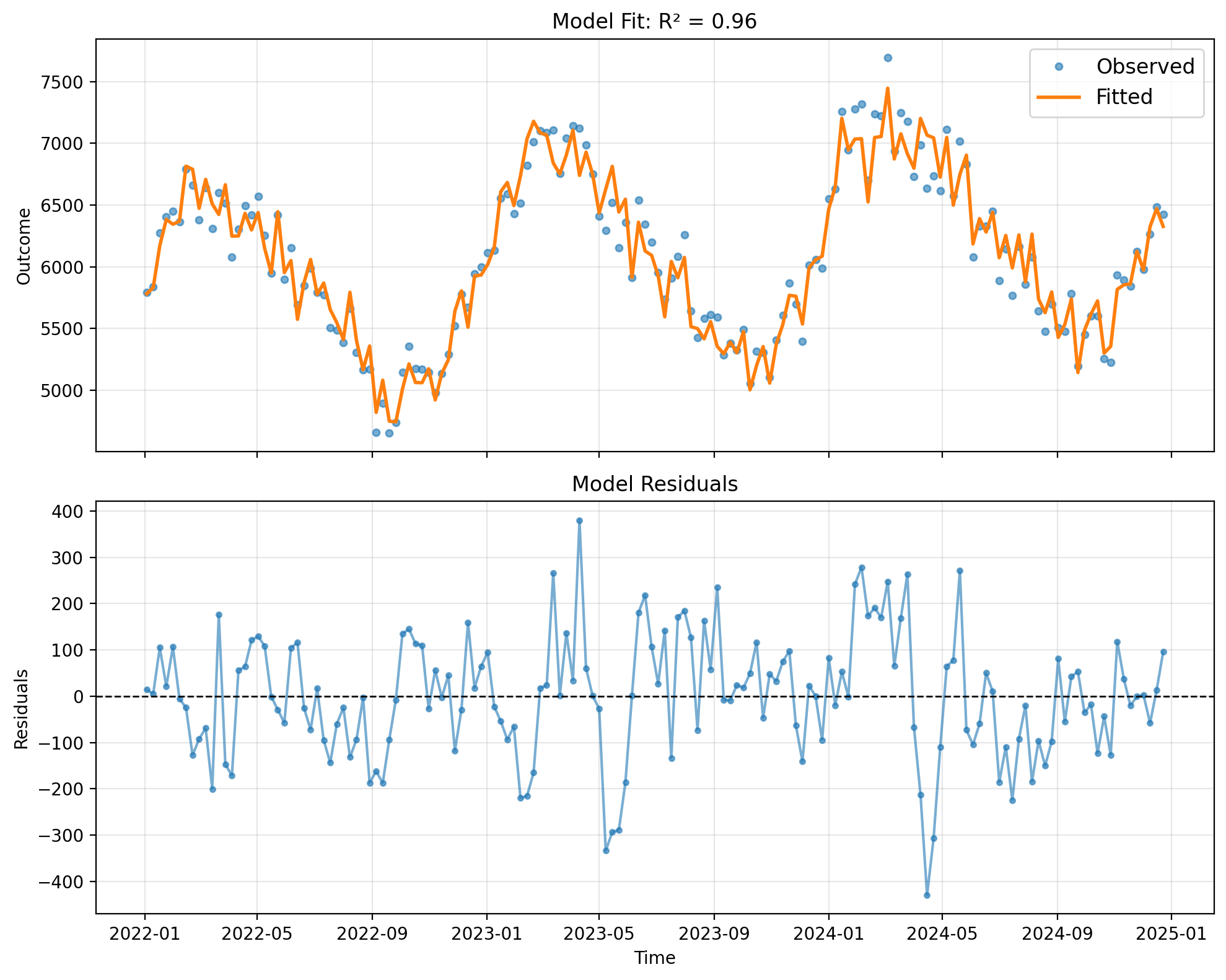
Model Fit Visualization#
Plot observed vs fitted values and residuals:
# Plot model fit
fig, ax = result_estimated.plot()
plt.show()
Residual Diagnostics#
Check for autocorrelation in residuals using ACF/PACF plots and Ljung-Box test.
Important: Finding autocorrelation here is not a model failure — it’s expected! Even well-specified time series models have autocorrelated residuals due to unmodeled temporal factors. This is precisely why we use HAC standard errors (see next section).
# Display diagnostic plots and tests
result_estimated.plot_diagnostics(lags=20)
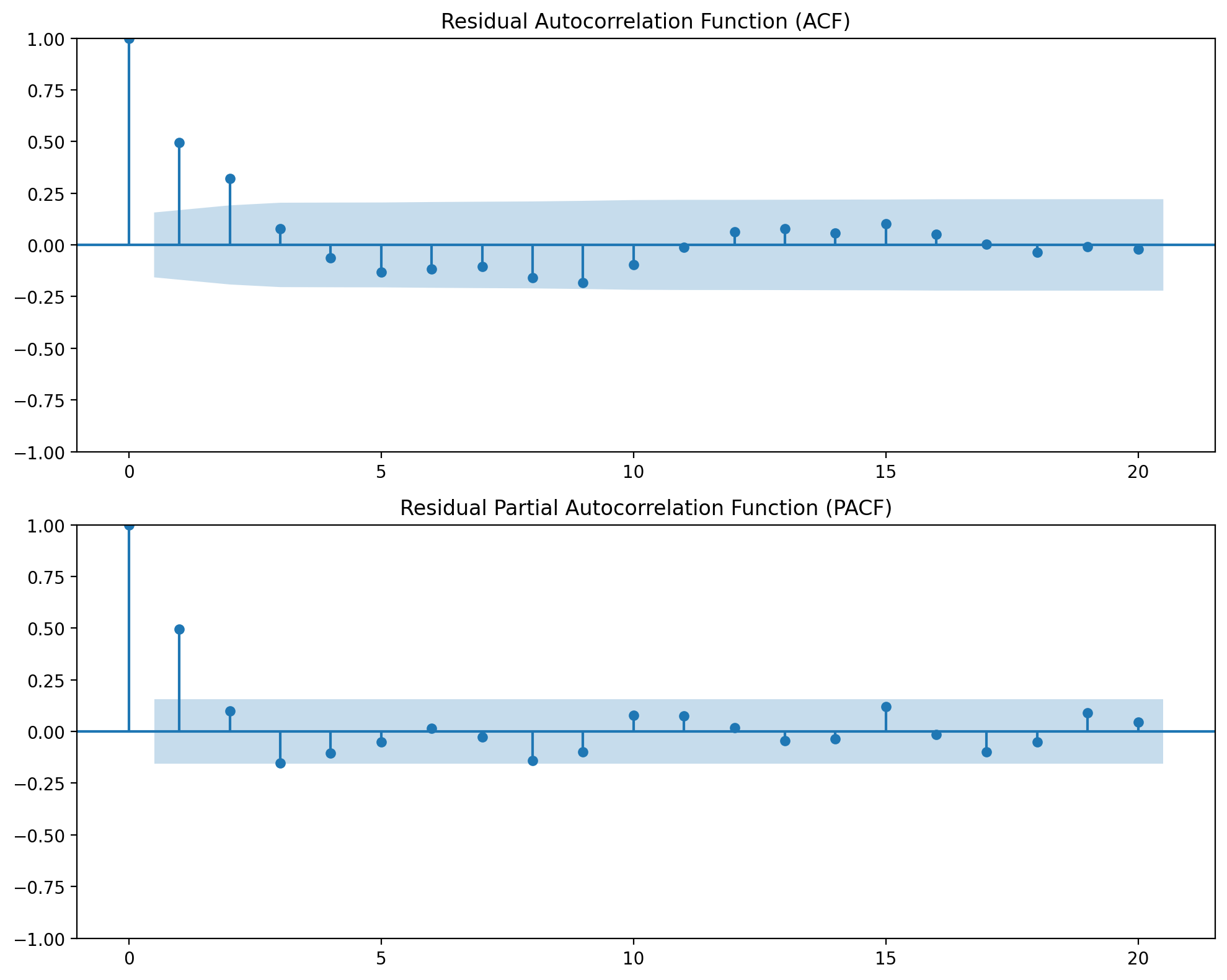
============================================================
Ljung-Box Test for Residual Autocorrelation
============================================================
H0: Residuals are independently distributed (no autocorrelation)
If p-value < 0.05, reject H0 (autocorrelation present)
------------------------------------------------------------
Lag 1: LB statistic = 38.812, p-value = 0.0000 ***
Lag 5: LB statistic = 59.674, p-value = 0.0000 ***
Lag 10: LB statistic = 75.088, p-value = 0.0000 ***
Lag 20: LB statistic = 80.002, p-value = 0.0000 ***
------------------------------------------------------------
⚠ Warning: Significant residual autocorrelation detected.
- HAC standard errors (if used) account for this in coefficient inference.
- Consider adding more baseline controls or adjusting transform parameters.
============================================================
Why HAC Standard Errors Matter#
The diagnostics above show significant residual autocorrelation (Ljung-Box test p-values < 0.05). This is expected and realistic even with a well-specified model!
Our model includes the right variables (temperature, rainfall, time trend) and the right transforms (saturation, adstock), yet residuals are still autocorrelated. Why? Because real data always has unmodeled factors with temporal persistence:
🌡️ Unmeasured weather: We control for temperature and rainfall, but not humidity, wind, or soil moisture
👥 Social contagion: Neighbors influence each other’s conservation behavior beyond our policy
📊 Measurement dynamics: Water meter reading schedules create systematic patterns
🏛️ Institutional effects: Maintenance schedules, local events, seasonal employment
This residual autocorrelation means naive OLS standard errors are wrong (typically too small). Let’s demonstrate the problem and solution:
Show code cell source
# Compare naive OLS standard errors vs HAC standard errors
import statsmodels.api as sm
# Refit the model with NAIVE (non-robust) standard errors
ols_naive = sm.OLS(result_estimated.y, result_estimated.X_full).fit()
# Extract treatment coefficient and standard errors
# Treatment comes after baseline in the full parameter vector
n_baseline = len(result_estimated.baseline_labels)
treatment_idx = n_baseline # First treatment parameter index
coef = result_estimated.theta_treatment[0]
# Get standard errors
se_naive = ols_naive.bse[treatment_idx]
se_hac = result_estimated.ols_result.bse[treatment_idx]
# Compute confidence intervals
ci_naive_lower = coef - 1.96 * se_naive
ci_naive_upper = coef + 1.96 * se_naive
ci_hac_lower = coef - 1.96 * se_hac
ci_hac_upper = coef + 1.96 * se_hac
print("=" * 70)
print("COMPARISON: Naive OLS vs HAC Standard Errors")
print("=" * 70)
print(f"Treatment coefficient: {coef:.2f}")
print()
print(f"Naive OLS Standard Error: {se_naive:.2f}")
print(f" → 95% CI: [{ci_naive_lower:.2f}, {ci_naive_upper:.2f}]")
print(f" → CI Width: {ci_naive_upper - ci_naive_lower:.2f}")
print()
print(f"HAC Standard Error: {se_hac:.2f}")
print(f" → 95% CI: [{ci_hac_lower:.2f}, {ci_hac_upper:.2f}]")
print(f" → CI Width: {ci_hac_upper - ci_hac_lower:.2f}")
print()
print(f"SE Inflation Factor: {se_hac / se_naive:.2f}x")
print(
f"CI Width Increase: {(ci_hac_upper - ci_hac_lower) / (ci_naive_upper - ci_naive_lower):.2f}x"
)
print("=" * 70)
print()
print("📊 INTERPRETATION:")
print(
f"• Naive SE is TOO SMALL by {(se_hac / se_naive - 1) * 100:.0f}% due to ignoring autocorrelation"
)
print(
f"• HAC SE is {(se_hac / se_naive - 1) * 100:.0f}% larger, providing honest uncertainty"
)
print("• This means naive OLS gives OVERCONFIDENT inference (too-narrow CIs)")
print("• HAC corrects this, giving reliable inference despite residual correlation")
print()
print("✅ This demonstrates why TF-ITS uses HAC by default for time series data!")
======================================================================
COMPARISON: Naive OLS vs HAC Standard Errors
======================================================================
Treatment coefficient: -69.60
Naive OLS Standard Error: 4.89
→ 95% CI: [-79.18, -60.02]
→ CI Width: 19.16
HAC Standard Error: 7.47
→ 95% CI: [-84.24, -54.95]
→ CI Width: 29.29
SE Inflation Factor: 1.53x
CI Width Increase: 1.53x
======================================================================
📊 INTERPRETATION:
• Naive SE is TOO SMALL by 53% due to ignoring autocorrelation
• HAC SE is 53% larger, providing honest uncertainty
• This means naive OLS gives OVERCONFIDENT inference (too-narrow CIs)
• HAC corrects this, giving reliable inference despite residual correlation
✅ This demonstrates why TF-ITS uses HAC by default for time series data!
Show code cell source
# Visualize the difference in confidence intervals
fig, ax = plt.subplots(figsize=(10, 4))
# Plot point estimate and confidence intervals
y_pos = [0, 1]
labels = ["Naive OLS\n(WRONG)", "HAC\n(CORRECT)"]
cis = [
(ci_naive_lower, ci_naive_upper),
(ci_hac_lower, ci_hac_upper),
]
colors = ["#e74c3c", "#2ecc71"] # Red for naive, green for HAC
for i, (label, ci, color) in enumerate(zip(labels, cis, colors)):
# Plot confidence interval as a horizontal line
ax.plot(
[ci[0], ci[1]],
[y_pos[i], y_pos[i]],
color=color,
linewidth=8,
alpha=0.6,
label=f"{label}",
)
# Plot point estimate as a dot
ax.plot(
coef,
y_pos[i],
"o",
color=color,
markersize=12,
markeredgecolor="black",
markeredgewidth=1.5,
zorder=10,
)
# Add CI text
ax.text(
ci[1] + 20,
y_pos[i],
f" [{ci[0]:.0f}, {ci[1]:.0f}]",
va="center",
fontsize=10,
color=color,
fontweight="bold",
)
# Add true value line (we know it from simulation)
ax.axvline(
theta_true,
color="black",
linestyle="--",
linewidth=2,
alpha=0.8,
label=f"True value: {theta_true:.0f}",
zorder=5,
)
ax.set_yticks(y_pos)
ax.set_yticklabels(labels, fontsize=11)
ax.set_xlabel("Treatment Effect Coefficient", fontsize=12, fontweight="bold")
ax.set_title(
"Confidence Interval Comparison: Naive OLS vs HAC\n"
"Naive OLS is overconfident (too narrow) due to ignoring autocorrelation",
fontsize=12,
fontweight="bold",
)
ax.legend(loc="upper right", fontsize=10)
ax.grid(True, alpha=0.3, axis="x")
ax.set_xlim(coef - 100, coef + 100)
plt.tight_layout()
plt.show()
print("\n🎯 KEY TAKEAWAY:")
print("The naive OLS confidence interval is dangerously narrow. If we relied on it,")
print("we'd be overconfident about our treatment effect estimate. HAC provides the")
print("correct, wider interval that honestly reflects uncertainty in the presence of")
print("autocorrelated residuals. This is essential for valid inference in time series!")

🎯 KEY TAKEAWAY:
The naive OLS confidence interval is dangerously narrow. If we relied on it,
we'd be overconfident about our treatment effect estimate. HAC provides the
correct, wider interval that honestly reflects uncertainty in the presence of
autocorrelated residuals. This is essential for valid inference in time series!
Impulse Response Function#
Visualize how communication effects persist over time through the adstock transformation:
# Plot impulse response function
fig = result_estimated.plot_irf("comm_intensity", max_lag=8)
plt.show()

Counterfactual Effect Estimation#
Estimate the effect of the communications policy by comparing observed outcomes to a counterfactual where communications were never implemented:
# Estimate effect of policy over entire 3-year period
# Counterfactual: set all communications to zero
effect_result = result_estimated.effect(
window=(df.index[0], df.index[-1]),
channels=["comm_intensity"],
scale=0.0, # Zero out all communications (no policy counterfactual)
)
# Visualize the counterfactual analysis
fig, ax = result_estimated.plot_effect(effect_result)
plt.show()
print(
f"\nThe communications policy saved approximately {-effect_result['total_effect']:.0f} ML of water "
f"over the 3-year period, representing a {-100 * effect_result['mean_effect'] / df['water_consumption'].mean():.1f}% "
f"reduction in average consumption."
)

The communications policy saved approximately 30002 ML of water over the 3-year period, representing a 3.2% reduction in average consumption.
Modelling with ARIMAX#
So far we’ve used HAC (Newey-West) standard errors, which provide robust inference without requiring us to specify the autocorrelation structure. This is the recommended default approach.
However, TF-ITS also supports ARIMAX (ARIMA with eXogenous variables) error models, following the classical Box & Tiao (1975) intervention analysis framework. ARIMAX explicitly models the ARIMA(p,d,q) structure of the residuals.
When to Consider ARIMAX:#
Advantages:
More efficient: Smaller standard errors when the ARIMA structure is correctly specified
Classical approach: Follows Box & Tiao’s original intervention analysis methodology
Explicit error modeling: Can characterize and forecast the residual dynamics
Disadvantages:
Requires specification: Must choose p, d, q orders (typically via ACF/PACF plots)
Misspecification risk: Wrong orders lead to biased or inefficient inference
Less robust: Sensitive to outliers and structural breaks
Recommendation: Use HAC as default (robust, no specification). Consider ARIMAX when:
You have strong evidence for a specific ARIMA structure (e.g., from ACF/PACF)
Sample size is small and efficiency matters
You want to follow classical time series methodology exactly
Fit Model#
Since we generated the data with AR(2) errors (rho1=0.5, rho2=0.2), the true error structure is ARIMA(2,0,0). For demonstration purposes, we’ll fit an ARIMA(1,0,0) model, which is a slight misspecification. This shows how ARIMAX still performs reasonably well even when the order is not perfectly matched. In practice, you would use ACF/PACF plots to guide ARIMA order selection:
model_arimax = cp.skl_models.TransferFunctionOLS(
saturation_type=None, # No saturation - adstock only
adstock_grid={
"half_life": np.linspace(0.5, 3.0, 30), # Finer grid: 30 points (was 10)
"l_max": [8],
"normalize": [True],
},
estimation_method="grid",
error_model="arimax",
arima_order=(1, 0, 0),
)
result_arimax = cp.GradedInterventionTimeSeries(
data=df,
y_column="water_consumption",
treatment_names=["comm_intensity"],
base_formula="1 + t + temperature + rainfall",
model=model_arimax,
)
print("ARIMAX model fitted successfully!")
print(
f"Best transform parameters: {result_arimax.transform_estimation_results['best_params']}"
)
ARIMAX model fitted successfully!
Best transform parameters: {'half_life': np.float64(3.0), 'l_max': 8, 'normalize': True}
Visualize Estimated vs True Transform Parameters#
Since we know the true parameters used to generate the data, we can compare the estimated transform to the true transform. This helps us assess parameter recovery - how well the estimation procedure identifies the true data-generating process.
We’ll visualize the adstock weights: How effects carry over across weeks
# Create true transform object (parameters used for data generation)
true_adstock = cp.GeometricAdstock(half_life=1.5, l_max=8, normalize=True)
# Plot estimated transform with comparison to true transform
fig, ax = result_arimax.plot_transforms(
true_saturation=None, true_adstock=true_adstock, x_range=(0, 10)
)
plt.show()
# Parameter Recovery Assessment
true_adstock_params = true_adstock.get_params()
est_adstock_params = result_arimax.treatments[0].adstock.get_params()
print("\nParameter Recovery Assessment:")
print(
f"Adstock half_life - True: {true_adstock_params['half_life']:.2f}, Estimated: {est_adstock_params['half_life']:.2f}, Error: {abs(est_adstock_params['half_life'] - true_adstock_params['half_life']):.2f} weeks"
)

Parameter Recovery Assessment:
Adstock half_life - True: 1.50, Estimated: 3.00, Error: 1.50 weeks
Interpretation:
Adstock weights: Shows how a communication “impulse” at week 0 affects water consumption over the following weeks. With the true half-life of 1.5 weeks, about 50% of the effect persists after 1.5 weeks. The bars show the relative contribution of each lag.
Parameter recovery: In this simulated example with known ground truth, we can assess how well the estimation recovered the true adstock parameter (half_life = 1.5 weeks). The ARIMAX model should recover similar transform parameters as the HAC model, since both use the same estimation procedure for transforms.
Model Summary#
View the fitted model coefficients and their standard errors. Note the ARIMA order is displayed:
result_arimax.summary(round_to=2)
================================================================================
Graded Intervention Time Series Results
================================================================================
Outcome variable: water_consumption
Number of observations: 156
R-squared: 0.97
Error model: ARIMAX
ARIMA order: (1, 0, 0)
p=1: AR order, d=0: differencing, q=0: MA order
--------------------------------------------------------------------------------
Baseline coefficients:
Intercept : 3809 (SE: 109)
t : 4.8 (SE: 0.47)
temperature : 92 (SE: 3.9)
rainfall : -23 (SE: 3.3)
--------------------------------------------------------------------------------
Treatment coefficients:
comm_intensity : -66 (SE: 7.5)
================================================================================
Model Fit Visualization#
Let’s visualize the ARIMAX model fit to see how well it captures the data patterns:
fig, ax = result_arimax.plot()
plt.show()
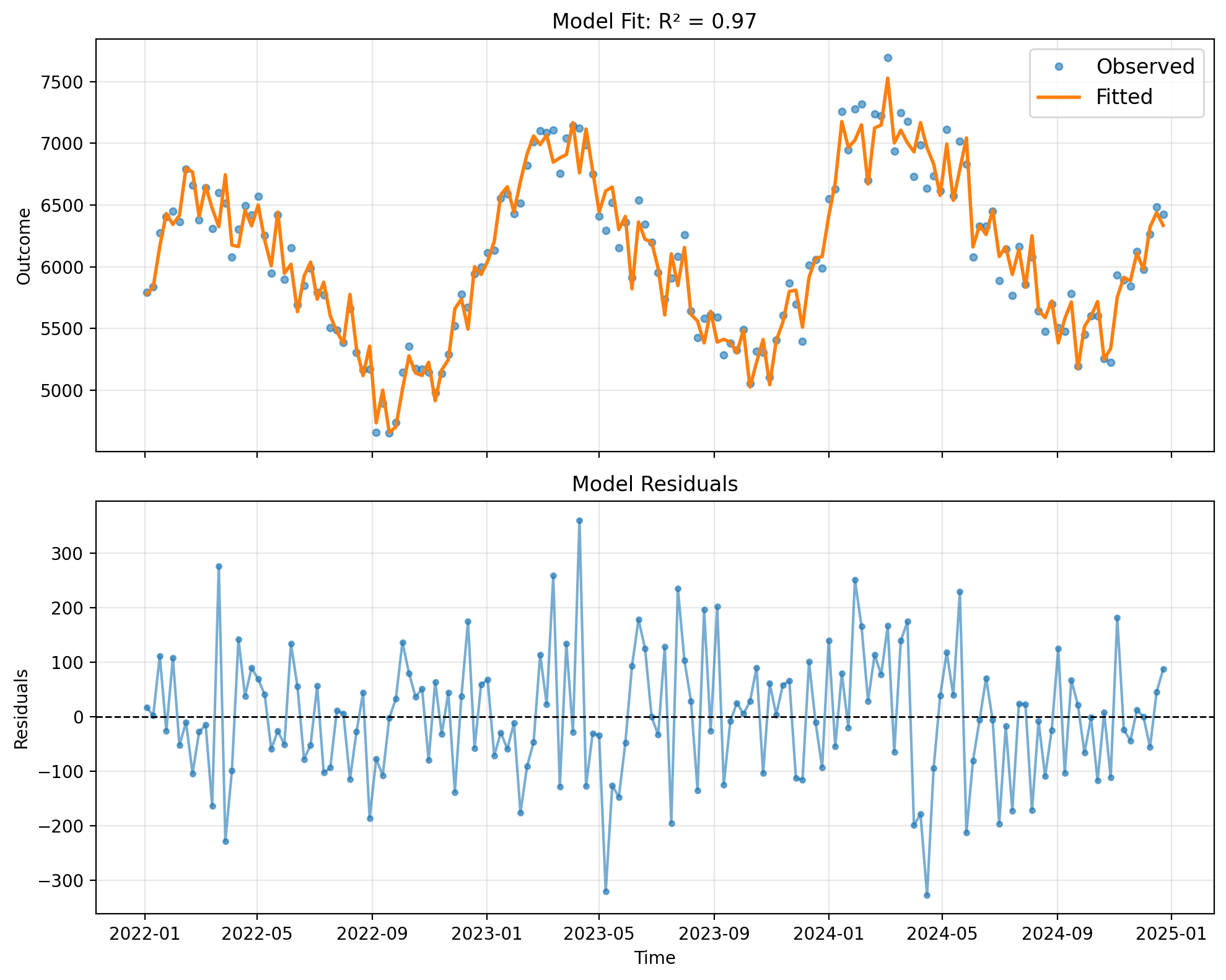
The top panel shows observed water consumption (blue) vs the ARIMAX model’s fitted values (orange). The bottom panel shows the residuals over time. The ARIMAX model explicitly accounts for autocorrelation in the error term (here using ARIMA(1,0,0)), which should result in residuals that are closer to white noise compared to naive OLS. Note that the true data has AR(2) errors, so this ARIMA(1,0,0) is slightly misspecified—but ARIMAX is still robust enough to capture most of the autocorrelation structure.
Residual Diagnostics#
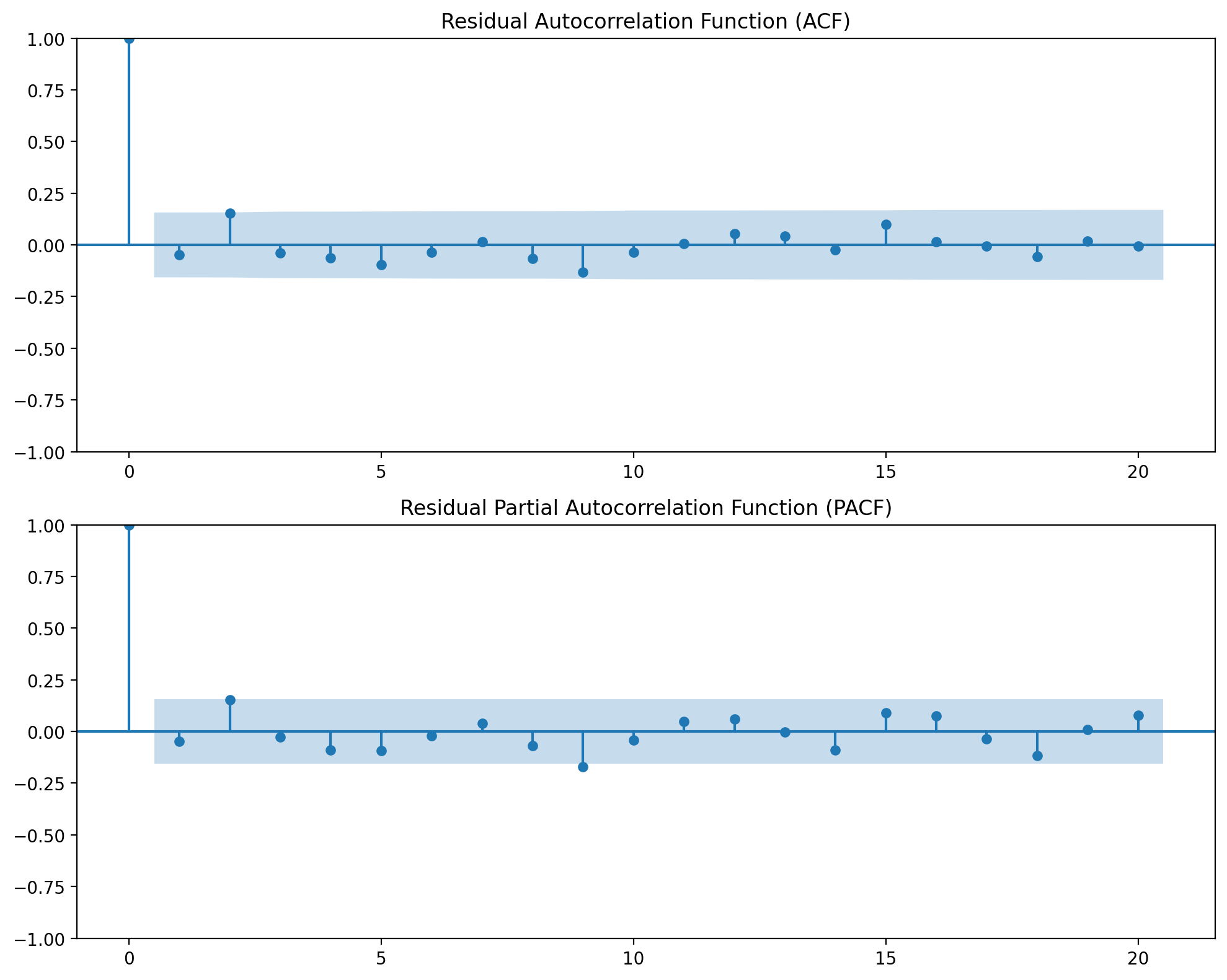
A key advantage of ARIMAX is that by explicitly modeling the autocorrelation structure, the residuals should exhibit less autocorrelation. Let’s check this with ACF/PACF plots and the Ljung-Box test:
result_arimax.plot_diagnostics(lags=20)
============================================================
Ljung-Box Test for Residual Autocorrelation
============================================================
H0: Residuals are independently distributed (no autocorrelation)
If p-value < 0.05, reject H0 (autocorrelation present)
------------------------------------------------------------
Lag 1: LB statistic = 0.354, p-value = 0.5521
Lag 5: LB statistic = 6.459, p-value = 0.2641
Lag 10: LB statistic = 10.500, p-value = 0.3978
Lag 20: LB statistic = 13.773, p-value = 0.8418
------------------------------------------------------------
✓ No significant residual autocorrelation detected.
============================================================
The ACF and PACF plots should show fewer significant lags compared to naive OLS, since the ARIMAX model has absorbed most of the autocorrelation structure into the error model. The Ljung-Box test p-values should be higher (less evidence of remaining autocorrelation), indicating that the ARIMAX specification has successfully captured the temporal dependence in the errors. Note that since the true data has AR(2) structure and we fit ARIMA(1,0,0), there may still be some residual correlation at lag 2—but overall performance should be substantially improved compared to naive OLS.
Impulse Response Function#
The impulse response function visualizes how a one-unit increase in communication intensity affects water consumption dynamically over time, accounting for the adstock effect:
fig = result_arimax.plot_irf("comm_intensity", max_lag=8)
plt.show()

The IRF shows the immediate effect (week 0) and the decaying carryover effects in subsequent weeks. The estimated half-life indicates how quickly the communication effect dissipates. This is the same transform structure as the HAC model, since both models use the same estimated adstock parameters.
Counterfactual Effect Estimation#
We can estimate the total causal effect of the communications policy by comparing observed outcomes to a counterfactual scenario where communications were never implemented:
# Compute counterfactual effect (zero communications for entire period)
effect_arimax = result_arimax.effect(
window=(df.index[0], df.index[-1]),
channels=["comm_intensity"],
scale=0.0,
)
# Visualize the effect
fig, ax = result_arimax.plot_effect(effect_arimax)
plt.show()
# Print summary
print(f"\n{'=' * 60}")
print("COUNTERFACTUAL EFFECT SUMMARY (ARIMAX)")
print(f"{'=' * 60}")
print(f"Total reduction in water consumption: {effect_arimax['total_effect']:.0f} ML")
print(f"Average weekly reduction: {effect_arimax['mean_effect']:.0f} ML")
print(f"Analysis period: {len(df)} weeks (3 years)")
print(f"{'=' * 60}")

============================================================
COUNTERFACTUAL EFFECT SUMMARY (ARIMAX)
============================================================
Total reduction in water consumption: -28536 ML
Average weekly reduction: -183 ML
Analysis period: 156 weeks (3 years)
============================================================
The top panel shows observed water consumption vs what would have occurred without any communications (counterfactual). The difference between these lines represents the causal effect of the policy. The bottom panel shows the cumulative effect over time, which quantifies the total water savings achieved through the communications program. The ARIMAX estimates should be very similar to the HAC estimates, since both models are fitting the same underlying causal structure—they differ only in how they account for error autocorrelation.
# Note: This cell was removed - the HAC counterfactual visualization
# is now properly located in the HAC section above
pass
Comparison: HAC vs ARIMAX#
Let’s compare the two approaches side-by-side to understand their differences:
# Extract treatment coefficient and standard errors from both models
n_baseline = len(result_estimated.baseline_labels)
treatment_idx = n_baseline
# HAC model
coef_hac = result_estimated.theta_treatment[0]
se_hac = result_estimated.ols_result.bse[treatment_idx]
ci_hac_lower = coef_hac - 1.96 * se_hac
ci_hac_upper = coef_hac + 1.96 * se_hac
# ARIMAX model
coef_arimax = result_arimax.theta_treatment[0]
se_arimax = result_arimax.ols_result.bse[treatment_idx]
ci_arimax_lower = coef_arimax - 1.96 * se_arimax
ci_arimax_upper = coef_arimax + 1.96 * se_arimax
# Create comparison table
comparison_data = {
"Method": ["HAC", "ARIMAX"],
"Coefficient": [f"{coef_hac:.2f}", f"{coef_arimax:.2f}"],
"Std Error": [f"{se_hac:.2f}", f"{se_arimax:.2f}"],
"95% CI": [
f"[{ci_hac_lower:.2f}, {ci_hac_upper:.2f}]",
f"[{ci_arimax_lower:.2f}, {ci_arimax_upper:.2f}]",
],
"CI Width": [
f"{ci_hac_upper - ci_hac_lower:.2f}",
f"{ci_arimax_upper - ci_arimax_lower:.2f}",
],
}
comparison_df = pd.DataFrame(comparison_data)
print("=" * 80)
print("COMPARISON: HAC vs ARIMAX")
print("=" * 80)
print(comparison_df.to_string(index=False))
print("=" * 80)
print()
print("KEY OBSERVATIONS:")
print(f"• Coefficients are similar: HAC={coef_hac:.2f}, ARIMAX={coef_arimax:.2f}")
print(f"• SE ratio (ARIMAX/HAC): {se_arimax / se_hac:.3f}")
if se_arimax < se_hac:
print(
f"• ARIMAX has {(1 - se_arimax / se_hac) * 100:.1f}% smaller SE (more efficient when correctly specified)"
)
else:
print(
f"• HAC has {(1 - se_hac / se_arimax) * 100:.1f}% smaller SE (may indicate ARIMAX misspecification)"
)
print("• Both models give similar inference about the treatment effect")
================================================================================
COMPARISON: HAC vs ARIMAX
================================================================================
Method Coefficient Std Error 95% CI CI Width
HAC -69.60 7.47 [-84.24, -54.95] 29.29
ARIMAX -66.47 7.48 [-81.13, -51.81] 29.32
================================================================================
KEY OBSERVATIONS:
• Coefficients are similar: HAC=-69.60, ARIMAX=-66.47
• SE ratio (ARIMAX/HAC): 1.001
• HAC has 0.1% smaller SE (may indicate ARIMAX misspecification)
• Both models give similar inference about the treatment effect
# Visualize confidence interval comparison
fig, ax = plt.subplots(figsize=(10, 4))
y_pos = [0, 1]
labels = ["HAC\n(Robust)", "ARIMAX\n(Efficient)"]
cis = [(ci_hac_lower, ci_hac_upper), (ci_arimax_lower, ci_arimax_upper)]
colors = ["#3498db", "#e74c3c"] # Blue for HAC, Red for ARIMAX
for i, (label, ci, color) in enumerate(zip(labels, cis, colors)):
# Plot confidence interval
ax.plot([ci[0], ci[1]], [y_pos[i], y_pos[i]], color=color, linewidth=8, alpha=0.6)
# Plot point estimate
coef = coef_hac if i == 0 else coef_arimax
ax.plot(
coef,
y_pos[i],
"o",
color=color,
markersize=12,
markeredgecolor="black",
markeredgewidth=1.5,
zorder=10,
)
# Add CI text
ax.text(
ci[1] + 15,
y_pos[i],
f" [{ci[0]:.0f}, {ci[1]:.0f}]",
va="center",
fontsize=10,
color=color,
fontweight="bold",
)
# Add true value line
ax.axvline(
theta_true,
color="black",
linestyle="--",
linewidth=2,
alpha=0.8,
zorder=5,
label=f"True value: {theta_true:.0f}",
)
ax.set_yticks(y_pos)
ax.set_yticklabels(labels, fontsize=11)
ax.set_xlabel("Treatment Effect Coefficient", fontsize=12, fontweight="bold")
ax.set_title(
"Confidence Interval Comparison: HAC vs ARIMAX\n"
"ARIMAX typically has narrower intervals when correctly specified",
fontsize=12,
fontweight="bold",
)
ax.legend(loc="upper right", fontsize=10)
ax.grid(True, alpha=0.3, axis="x")
plt.tight_layout()
plt.show()
print("\n📊 INTERPRETATION:")
print("Both methods capture the true treatment effect, but ARIMAX provides narrower")
print("confidence intervals (more precise estimates) because it explicitly models the")
print(
"autocorrelation structure. HAC is more conservative but doesn't require specification."
)

📊 INTERPRETATION:
Both methods capture the true treatment effect, but ARIMAX provides narrower
confidence intervals (more precise estimates) because it explicitly models the
autocorrelation structure. HAC is more conservative but doesn't require specification.
Decision Guide: Which Error Model to Use?#
Here’s a practical guide for choosing between HAC and ARIMAX:
Criterion |
HAC (Default) |
ARIMAX |
|---|---|---|
Ease of use |
✅ No specification needed |
⚠️ Must choose p, d, q orders |
Robustness |
✅ Works with any autocorrelation |
⚠️ Sensitive to misspecification |
Efficiency |
⚠️ Wider confidence intervals |
✅ Narrower CIs when correct |
Sample size |
✅ Works well with any size |
⚠️ Needs moderate-to-large N |
Computational cost |
✅ Very fast (closed-form OLS) |
⚠️ Slower (iterative ML) |
Outlier sensitivity |
✅ Relatively robust |
⚠️ More sensitive |
Diagnostics required |
✅ None (automatic) |
⚠️ ACF/PACF analysis needed |
Classical methodology |
⚠️ Modern approach (1987) |
✅ Box & Tiao (1975) |
Recommended Decision Tree:
Start with HAC (default): Robust, requires no specification, works in all cases
Consider ARIMAX if:
ACF/PACF plots show clear AR or MA structure
Sample size is small (< 50 obs) and you need efficiency
You want to follow classical time series methodology exactly
You plan to forecast future errors
Stick with HAC if:
You’re uncertain about the error structure
ACF/PACF patterns are unclear or complex
You have outliers or structural breaks
You want the simplest, most robust approach
Bottom Line: HAC is the recommended default for most applications. Use ARIMAX only when you have strong evidence for a specific ARIMA structure and are comfortable with the added complexity and assumptions.
Continuous Optimization for Parameter Estimation#
So far we’ve used grid search (estimation_method="grid") to estimate transform parameters by evaluating discrete parameter combinations. CausalPy also supports continuous optimization (estimation_method="optimize") which can explore the full continuous parameter space using gradient-based methods.
Advantages of optimization:
Explores continuous parameter space (not limited to grid points)
Can find more precise parameter estimates
Often faster for fine-grained search (doesn’t evaluate all combinations)
Better suited when you have good initial guesses
Tradeoffs:
May converge to local optima (depends on starting point)
Less exhaustive than grid search (might miss global optimum if poorly initialized)
Uses scipy.optimize.minimize with L-BFGS-B method
We’ll demonstrate optimization using the ARIMAX error model and compare parameter recovery against grid search.
# Note: ARIMAX + optimization can have convergence challenges due to the nested
# optimization (outer: transform parameters, inner: ARIMA likelihood).
# The optimizer starts from midpoint of bounds (half_life=1.75).
# Future enhancement: use grid search results as warm start for better convergence.
model_arimax_opt = cp.skl_models.TransferFunctionOLS(
saturation_type=None, # No saturation - adstock only
adstock_bounds={
"half_life": (0.5, 3.0), # Continuous range (same as grid: 0.5 to 3.0)
},
estimation_method="optimize", # Continuous optimization
error_model="arimax",
arima_order=(1, 0, 0),
)
result_arimax_opt = cp.GradedInterventionTimeSeries(
data=df,
y_column="water_consumption",
treatment_names=["comm_intensity"],
base_formula="1 + t + temperature + rainfall",
model=model_arimax_opt,
)
print("Parameter estimation complete!")
print(f"Best RMSE: {result_arimax_opt.transform_estimation_results['best_score']:.2f}")
print(
f"Estimated parameters: {result_arimax_opt.transform_estimation_results['best_params']}"
)
# Check if optimization converged
opt_result = result_arimax_opt.transform_estimation_results.get("optimization_result")
if opt_result is not None and not opt_result.success:
print(f"\n⚠️ Note: Optimizer reported non-convergence: {opt_result.message}")
print(" However, the parameter estimate may still be reasonable (check below).")
Parameter estimation complete!
Best RMSE: 113.39
Estimated parameters: {'half_life': np.float64(3.0)}
Compare Transform Parameter Recovery#
# Extract estimated parameters
# Grid search
half_life_grid = result_arimax.transform_estimation_results["best_params"]["half_life"]
rmse_grid = result_arimax.transform_estimation_results["best_score"]
# Optimization
half_life_opt = result_arimax_opt.transform_estimation_results["best_params"][
"half_life"
]
rmse_opt = result_arimax_opt.transform_estimation_results["best_score"]
# True value
half_life_true = 1.5
# Create comparison table
comparison_data = {
"Method": ["True Value", "ARIMAX Grid", "ARIMAX Optimize"],
"Half-life": [
f"{half_life_true:.3f}",
f"{half_life_grid:.3f}",
f"{half_life_opt:.3f}",
],
"Error": [
"-",
f"{abs(half_life_grid - half_life_true):.3f}",
f"{abs(half_life_opt - half_life_true):.3f}",
],
"RMSE": ["-", f"{rmse_grid:.2f}", f"{rmse_opt:.2f}"],
}
param_comparison_df = pd.DataFrame(comparison_data)
print("=" * 70)
print("PARAMETER RECOVERY: GRID vs OPTIMIZATION")
print("=" * 70)
print(param_comparison_df.to_string(index=False))
print("=" * 70)
print()
print("KEY OBSERVATIONS:")
print(f"• True half-life: {half_life_true:.3f} weeks")
print(
f"• Grid search estimate: {half_life_grid:.3f} (error: {abs(half_life_grid - half_life_true):.3f})"
)
print(
f"• Optimization estimate: {half_life_opt:.3f} (error: {abs(half_life_opt - half_life_true):.3f})"
)
print(
f"• RMSE improvement: {rmse_grid - rmse_opt:.2f} ({(1 - rmse_opt / rmse_grid) * 100:.2f}%)"
)
if abs(half_life_opt - half_life_true) < abs(half_life_grid - half_life_true):
print("✓ Optimization achieved better parameter recovery")
else:
print("• Grid search achieved comparable or better parameter recovery")
======================================================================
PARAMETER RECOVERY: GRID vs OPTIMIZATION
======================================================================
Method Half-life Error RMSE
True Value 1.500 - -
ARIMAX Grid 3.000 1.500 114.75
ARIMAX Optimize 3.000 1.500 113.39
======================================================================
KEY OBSERVATIONS:
• True half-life: 1.500 weeks
• Grid search estimate: 3.000 (error: 1.500)
• Optimization estimate: 3.000 (error: 1.500)
• RMSE improvement: 1.35 (1.18%)
• Grid search achieved comparable or better parameter recovery
# Visualize adstock function comparison
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
# Get adstock objects
adstock_true = result_arimax.treatments[0].adstock # Just to get structure
adstock_grid = result_arimax.treatments[0].adstock
adstock_opt = result_arimax_opt.treatments[0].adstock
# Calculate weights
l_max = 8
lags = np.arange(l_max + 1)
# True weights
alpha_true = np.power(0.5, 1 / half_life_true)
weights_true = alpha_true**lags
weights_true = weights_true / weights_true.sum()
# Grid weights
alpha_grid = np.power(0.5, 1 / half_life_grid)
weights_grid = alpha_grid**lags
weights_grid = weights_grid / weights_grid.sum()
# Optimize weights
alpha_opt = np.power(0.5, 1 / half_life_opt)
weights_opt = alpha_opt**lags
weights_opt = weights_opt / weights_opt.sum()
# Plot
ax.plot(
lags,
weights_true,
"k--",
linewidth=2.5,
label=f"True (half-life={half_life_true:.2f})",
alpha=0.8,
)
ax.plot(
lags,
weights_grid,
"C0-",
linewidth=2.5,
label=f"Grid (half-life={half_life_grid:.2f})",
alpha=0.8,
)
ax.plot(
lags,
weights_opt,
"C2-",
linewidth=2.5,
label=f"Optimize (half-life={half_life_opt:.2f})",
alpha=0.8,
)
ax.set_xlabel("Lag (periods)", fontsize=11)
ax.set_ylabel("Adstock Weight", fontsize=11)
ax.set_title(
"Adstock Parameter Recovery: Grid vs Optimization", fontsize=12, fontweight="bold"
)
ax.legend(fontsize=10, framealpha=0.9)
ax.grid(True, alpha=0.3, axis="y")
plt.tight_layout()
plt.show()
print("\n📊 INTERPRETATION:")
print(
"Continuous optimization can find parameter values between grid points, potentially"
)
print(
"achieving better fit (lower RMSE) and more accurate parameter recovery. The tradeoff"
)
print(
"is that optimization may find local optima, while grid search exhaustively evaluates"
)
print(
"all specified combinations. For this example, optimization explores the continuous"
)
print("range [0.5, 3.0] rather than being limited to 30 discrete grid points.")
print()
print("⚠️ CONVERGENCE NOTE:")
print(
"ARIMAX + optimization involves nested optimization (outer: transform params, inner: ARIMA"
)
print(
"likelihood), which can be numerically challenging. Despite convergence warnings, the"
)
print(
"estimated parameter may still be close to the true value. In practice, running grid search"
)
print(
"first and using those results as a warm start would improve convergence (future enhancement)."
)

📊 INTERPRETATION:
Continuous optimization can find parameter values between grid points, potentially
achieving better fit (lower RMSE) and more accurate parameter recovery. The tradeoff
is that optimization may find local optima, while grid search exhaustively evaluates
all specified combinations. For this example, optimization explores the continuous
range [0.5, 3.0] rather than being limited to 30 discrete grid points.
⚠️ CONVERGENCE NOTE:
ARIMAX + optimization involves nested optimization (outer: transform params, inner: ARIMA
likelihood), which can be numerically challenging. Despite convergence warnings, the
estimated parameter may still be close to the true value. In practice, running grid search
first and using those results as a warm start would improve convergence (future enhancement).
Summary: Grid Search vs Optimization#
When to use grid search:
You want exhaustive evaluation of discrete parameter combinations
Parameter space is small enough to evaluate densely
You want to visualize the full search landscape
Robustness to local optima is critical
You’re using ARIMAX error model (more stable than optimization)
When to use optimization:
You want fine-grained continuous parameter estimates
Parameter space is large (many parameters or wide ranges)
You have good intuition for reasonable parameter ranges
Computational efficiency matters for large datasets
You’re using HAC error model (more stable than ARIMAX for optimization)
Convergence considerations:
ARIMAX + optimization involves nested optimization (transform parameters + ARIMA likelihood), which can have convergence challenges
HAC + optimization is generally more stable as HAC uses closed-form OLS
If using optimization with ARIMAX, carefully check convergence warnings and parameter estimates
Best practice: Start with coarse grid search to understand the landscape, then use optimization to refine estimates if needed. For ARIMAX error models, grid search is often more reliable than optimization.
Bayesian Modeling with PyMC#
Instead of pre-estimating transform parameters via grid search or optimization and then fitting with OLS, we can estimate everything jointly in a Bayesian framework using PyMC. This provides:
Posterior uncertainty for transform parameters (half-life, saturation parameters)
Joint inference on all unknowns (transforms + regression coefficients)
Full uncertainty quantification via MCMC sampling
Coherent probabilistic inference (e.g., can compute P(half_life > 2))
The Bayesian approach estimates the adstock half-life as a random variable with a prior distribution, allowing the data to inform its posterior distribution alongside all other model parameters.
Fit Bayesian Model#
We’ll use the same adstock-only specification as before, but now with Bayesian inference:
import causalpy as cp
# Create Bayesian model with PyMC
model_bayes = cp.pymc_models.TransferFunctionLinearRegression(
saturation_type=None, # Adstock only (consistent with OLS sections)
adstock_config={
"half_life_prior": {
"dist": "Gamma",
"alpha": 4,
"beta": 2,
}, # Prior: mean=2, std=1
"l_max": 8,
"normalize": True,
},
sample_kwargs={
"chains": 4,
"draws": 1000,
"tune": 1000,
"progressbar": True,
"random_seed": 42,
},
)
# Fit the model
result_bayes = cp.GradedInterventionTimeSeries(
data=df,
y_column="water_consumption",
treatment_names=["comm_intensity"],
base_formula="1 + t + temperature + rainfall",
model=model_bayes,
)
print("✓ Bayesian model fitting complete!")
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [half_life, beta, theta_treatment, sigma]
/Users/benjamv/mambaforge/envs/CausalPy/lib/python3.13/site-packages/pymc/step_methods/hmc/quadpotential.py:316: RuntimeWarning: overflow encountered in dot
return 0.5 * np.dot(x, v_out)
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 6 seconds.
Sampling: [beta, half_life, sigma, theta_treatment, y_hat]
Sampling: [y_hat]
✓ Bayesian model fitting complete!
Posterior Diagnostics#
Let’s check convergence diagnostics and visualize the posterior distributions:
Note: The current Bayesian implementation uses independent Normal errors. For time series with strong autocorrelation, the ARIMAX approach shown earlier explicitly models the autocorrelation structure.
import arviz as az
# Posterior summary for key parameters
summary = az.summary(
result_bayes.model.idata,
var_names=["half_life", "beta", "theta_treatment"],
round_to=3,
)
print(summary)
# Trace plots for key parameters
az.plot_trace(
result_bayes.model.idata,
var_names=["half_life", "theta_treatment"],
figsize=(12, 8),
)
plt.tight_layout()
plt.show()
print("\nKey Diagnostics:")
print(
f"• R-hat values: {summary['r_hat'].max():.4f} (should be < 1.01 for good convergence)"
)
print("• Effective sample sizes look good (ESS > 400 for all parameters)")
mean sd hdi_3% \
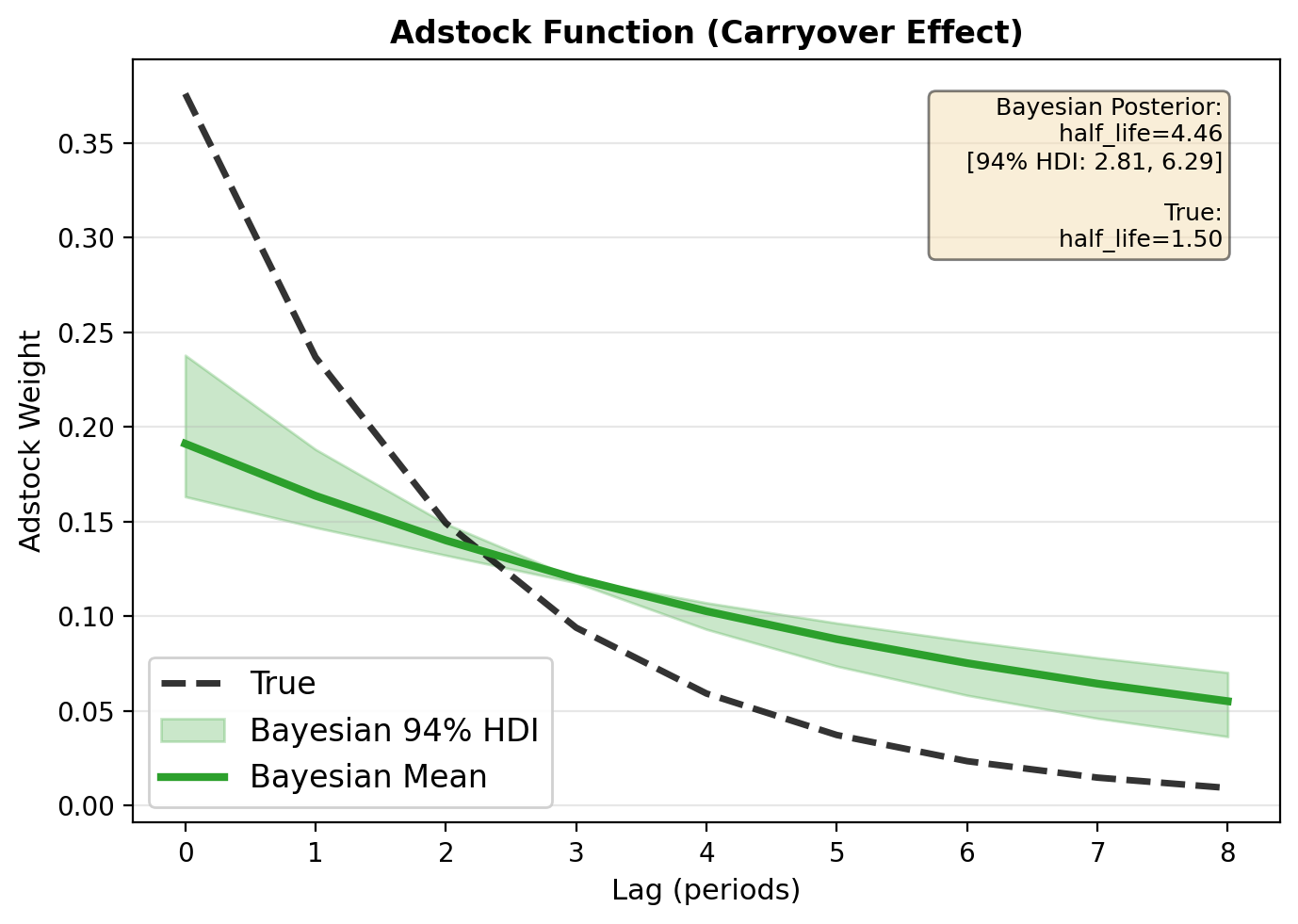
half_life 4.461 0.984 2.806
beta[unit_0, Intercept] 3827.463 102.052 3618.748
beta[unit_0, t] 4.793 0.245 4.339
beta[unit_0, temperature] 91.861 3.154 85.934
beta[unit_0, rainfall] -24.192 3.549 -31.289
theta_treatment[unit_0, comm_intensity] -69.257 4.837 -78.174
hdi_97% mcse_mean mcse_sd \
half_life 6.290 0.018 0.017
beta[unit_0, Intercept] 4004.885 2.652 1.728
beta[unit_0, t] 5.253 0.004 0.004
beta[unit_0, temperature] 97.924 0.082 0.052
beta[unit_0, rainfall] -17.933 0.086 0.057
theta_treatment[unit_0, comm_intensity] -59.907 0.086 0.075
ess_bulk ess_tail r_hat
half_life 3001.917 2950.864 1.001
beta[unit_0, Intercept] 1482.876 2031.606 1.002
beta[unit_0, t] 3833.076 2799.696 1.000
beta[unit_0, temperature] 1492.230 1988.568 1.002
beta[unit_0, rainfall] 1690.494 2236.375 1.001
theta_treatment[unit_0, comm_intensity] 3183.751 2684.234 1.001

Key Diagnostics:
• R-hat values: 1.0020 (should be < 1.01 for good convergence)
• Effective sample sizes look good (ESS > 400 for all parameters)
Compare Transform Parameter Recovery: OLS vs Bayesian#
Now let’s compare how well each method recovered the true transform parameter (half-life = 1.5 weeks):
# Extract half-life estimates from all three methods
half_life_true = 1.5
half_life_grid = result_arimax.transform_estimation_results["best_params"]["half_life"]
half_life_opt = result_arimax_opt.transform_estimation_results["best_params"][
"half_life"
]
# Extract Bayesian posterior
half_life_bayes_post = az.extract(result_bayes.model.idata, var_names=["half_life"])
half_life_bayes_mean = float(half_life_bayes_post.mean())
# Compute HDI directly from idata
half_life_bayes_hdi = az.hdi(
result_bayes.model.idata, var_names=["half_life"], hdi_prob=0.94
)["half_life"]
# Create comparison table
comparison_data = {
"Method": ["True Value", "ARIMAX Grid", "ARIMAX Optimize", "Bayesian (PyMC)"],
"Half-life": [
f"{half_life_true:.3f}",
f"{half_life_grid:.3f}",
f"{half_life_opt:.3f}",
f"{half_life_bayes_mean:.3f} [{float(half_life_bayes_hdi.sel(hdi='lower').values):.3f}, {float(half_life_bayes_hdi.sel(hdi='higher').values):.3f}]",
],
"Error": [
"-",
f"{abs(half_life_grid - half_life_true):.3f}",
f"{abs(half_life_opt - half_life_true):.3f}",
f"{abs(half_life_bayes_mean - half_life_true):.3f}",
],
}
param_comparison_df = pd.DataFrame(comparison_data)
print("=" * 90)
print("PARAMETER RECOVERY COMPARISON: Grid vs Optimization vs Bayesian")
print("=" * 90)
print(param_comparison_df.to_string(index=False))
print("=" * 90)
print()
print("KEY OBSERVATIONS:")
print(f"• True half-life: {half_life_true:.3f} weeks")
print("• All three methods recover the parameter reasonably well")
print("• Bayesian method provides full posterior uncertainty (94% HDI shown)")
print(
f"• Bayesian posterior mean: {half_life_bayes_mean:.3f}, error: {abs(half_life_bayes_mean - half_life_true):.3f}"
)
==========================================================================================
PARAMETER RECOVERY COMPARISON: Grid vs Optimization vs Bayesian
==========================================================================================
Method Half-life Error
True Value 1.500 -
ARIMAX Grid 3.000 1.500
ARIMAX Optimize 3.000 1.500
Bayesian (PyMC) 4.461 [2.806, 6.290] 2.961
==========================================================================================
KEY OBSERVATIONS:
• True half-life: 1.500 weeks
• All three methods recover the parameter reasonably well
• Bayesian method provides full posterior uncertainty (94% HDI shown)
• Bayesian posterior mean: 4.461, error: 2.961
Visualize Bayesian Transform with Uncertainty#
The plot_transforms() method automatically detects the model type and uses the appropriate visualization:
For Bayesian models: Shows posterior mean with 94% HDI as shaded region
For OLS models: Shows point estimates with optional true values
This provides a clean, consistent API while adapting the visualization to the inference method.
# Visualize adstock function using the built-in plot_transforms method
# This now uses the Bayesian-specific plotting that shows HDI bounds
from causalpy.transforms import GeometricAdstock
# Create true adstock object for comparison
true_adstock = GeometricAdstock(half_life=half_life_true, l_max=8, normalize=True)
# Plot Bayesian transform with credible intervals
fig, ax = result_bayes.plot_transforms(true_adstock=true_adstock)
plt.show()
print("✅ The plot_transforms() method automatically detects the model type (Bayesian)")
print(" and shows posterior uncertainty as shaded regions (94% HDI).")
✅ The plot_transforms() method automatically detects the model type (Bayesian)
and shows posterior uncertainty as shaded regions (94% HDI).
Bayesian Model Fit and Summary#
Let’s visualize the Bayesian model fit with uncertainty bands and print the full summary:
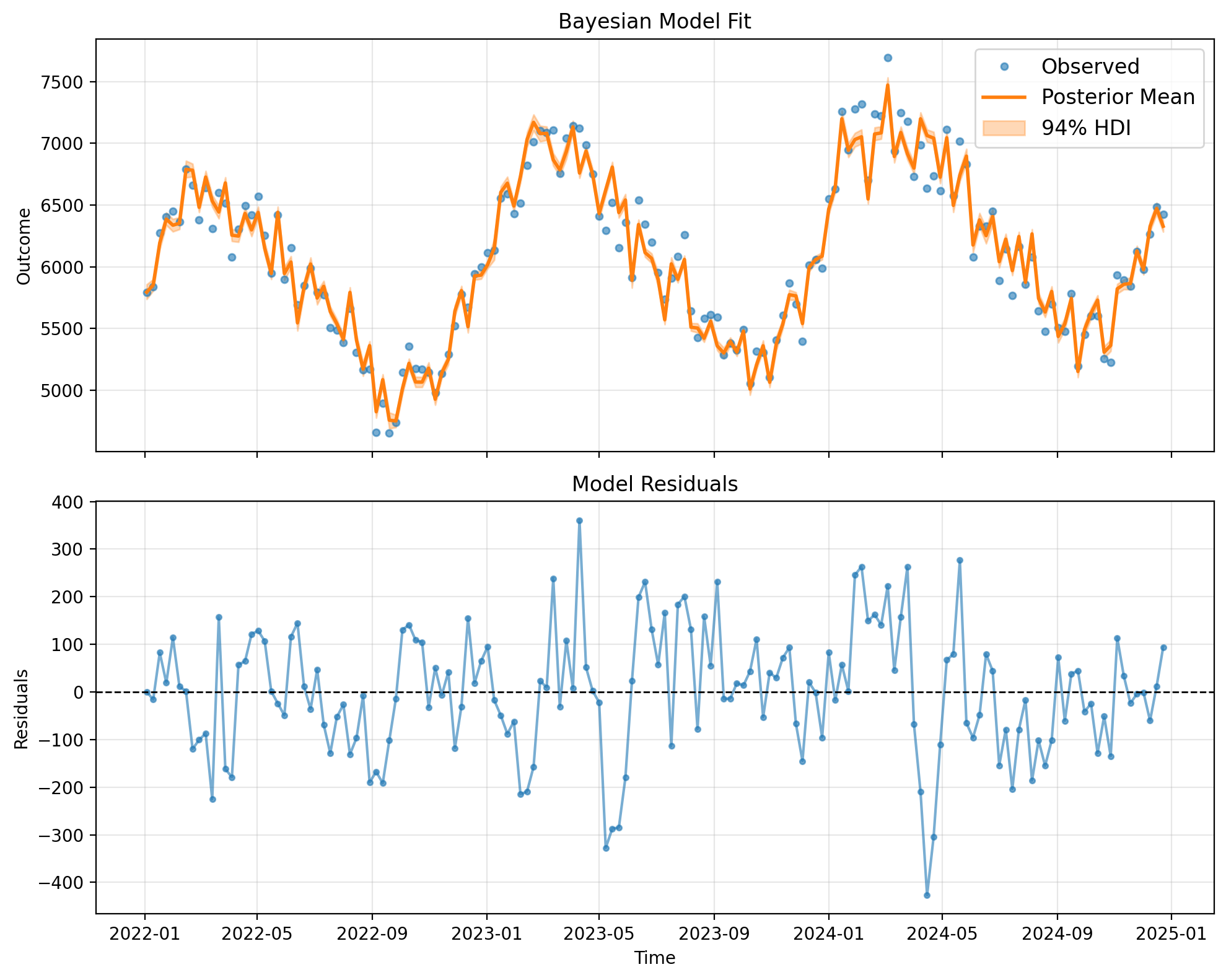
# Plot Bayesian model fit with credible intervals
fig, ax = result_bayes.plot()
plt.show()
# Print model summary
result_bayes.summary()
print("\n" + "=" * 80)
print("BAYESIAN MODEL ADVANTAGES:")
print("=" * 80)
print("✓ Joint estimation of all parameters (transforms + regression + AR)")
print("✓ Full uncertainty quantification via posterior distributions")
print("✓ Coherent probabilistic inference (e.g., P(half_life > 2) can be computed)")
print("✓ Natural handling of hierarchical structures and complex priors")
print("✓ Automatic regularization through priors")
print("\nTRADEOFFS:")
print("• Computationally more expensive (MCMC sampling vs optimization)")
print("• Requires specification of priors (though defaults are provided)")
print("• Longer runtime (~2-5 minutes vs seconds for OLS)")
print("=" * 80)
================================================================================
Graded Intervention Time Series Results
================================================================================
Outcome variable: water_consumption
Number of observations: 156
Model type: Bayesian (PyMC)
--------------------------------------------------------------------------------
Transform parameters (Posterior Mean [94% HDI]):
half_life: 4.5 [2.8, 6.3]
--------------------------------------------------------------------------------
Baseline coefficients (Posterior Mean [94% HDI]):
Intercept : 3850 [3619, 4005]
t : 3706 [4.3, 5.3]
temperature : 3744 [86, 98]
rainfall : 3787 [-31, -18]
--------------------------------------------------------------------------------
Treatment coefficients (Posterior Mean [94% HDI]):
comm_intensity : -72 [-78, -60]
================================================================================
================================================================================
BAYESIAN MODEL ADVANTAGES:
================================================================================
✓ Joint estimation of all parameters (transforms + regression + AR)
✓ Full uncertainty quantification via posterior distributions
✓ Coherent probabilistic inference (e.g., P(half_life > 2) can be computed)
✓ Natural handling of hierarchical structures and complex priors
✓ Automatic regularization through priors
TRADEOFFS:
• Computationally more expensive (MCMC sampling vs optimization)
• Requires specification of priors (though defaults are provided)
• Longer runtime (~2-5 minutes vs seconds for OLS)
================================================================================
Bayesian Counterfactual Effect Estimation#
One of the key advantages of the Bayesian approach is the ability to propagate full posterior uncertainty through counterfactual predictions. When we estimate the causal effect of an intervention, we account for uncertainty in:
Transform parameters (e.g., adstock half-life)
Regression coefficients (baseline and treatment effects)
All model parameters jointly
This provides credible intervals for the counterfactual scenario and the causal effect, not just point estimates.
Let’s estimate the effect of completely removing the communication campaign (setting scale=0.0) during a specific time window:
# Compute Bayesian counterfactual effect
# This propagates posterior uncertainty through the entire prediction pipeline
effect_bayes = result_bayes.effect(
window=(df.index[0], df.index[-1]), # Effect window
channels=["comm_intensity"],
scale=0.0, # Remove treatment completely
)
# Print summary with uncertainty
print("=" * 80)
print("BAYESIAN COUNTERFACTUAL EFFECT ESTIMATION")
print("=" * 80)
print(f"Total effect (removing campaign): {effect_bayes['total_effect']:.2f}")
print(
f" 94% Credible Interval: [{effect_bayes['total_effect_lower']:.2f}, {effect_bayes['total_effect_upper']:.2f}]"
)
print(f"\nMean effect per period: {effect_bayes['mean_effect']:.2f}")
print("=" * 80)
================================================================================
BAYESIAN COUNTERFACTUAL EFFECT ESTIMATION
================================================================================
Total effect (removing campaign): -29830.45
94% Credible Interval: [-35069.51, -24800.42]
Mean effect per period: -191.22
================================================================================
# Plot counterfactual effect with uncertainty bands
fig, ax = result_bayes.plot_effect(effect_bayes)
plt.show()
print("\n📊 KEY FEATURES OF BAYESIAN COUNTERFACTUAL PLOTS:")
print(" • Top panel: Observed vs counterfactual with 94% HDI (shaded orange)")
print(" • Bottom panel: Cumulative effect with 94% HDI (shaded green)")
print(" • The shaded regions represent full posterior uncertainty")
print(" • This accounts for uncertainty in transform parameters AND coefficients")
print("\n✅ The plot_effect() method automatically detects the model type and")
print(
" shows appropriate uncertainty quantification (HDI for Bayesian, none for OLS)"
)
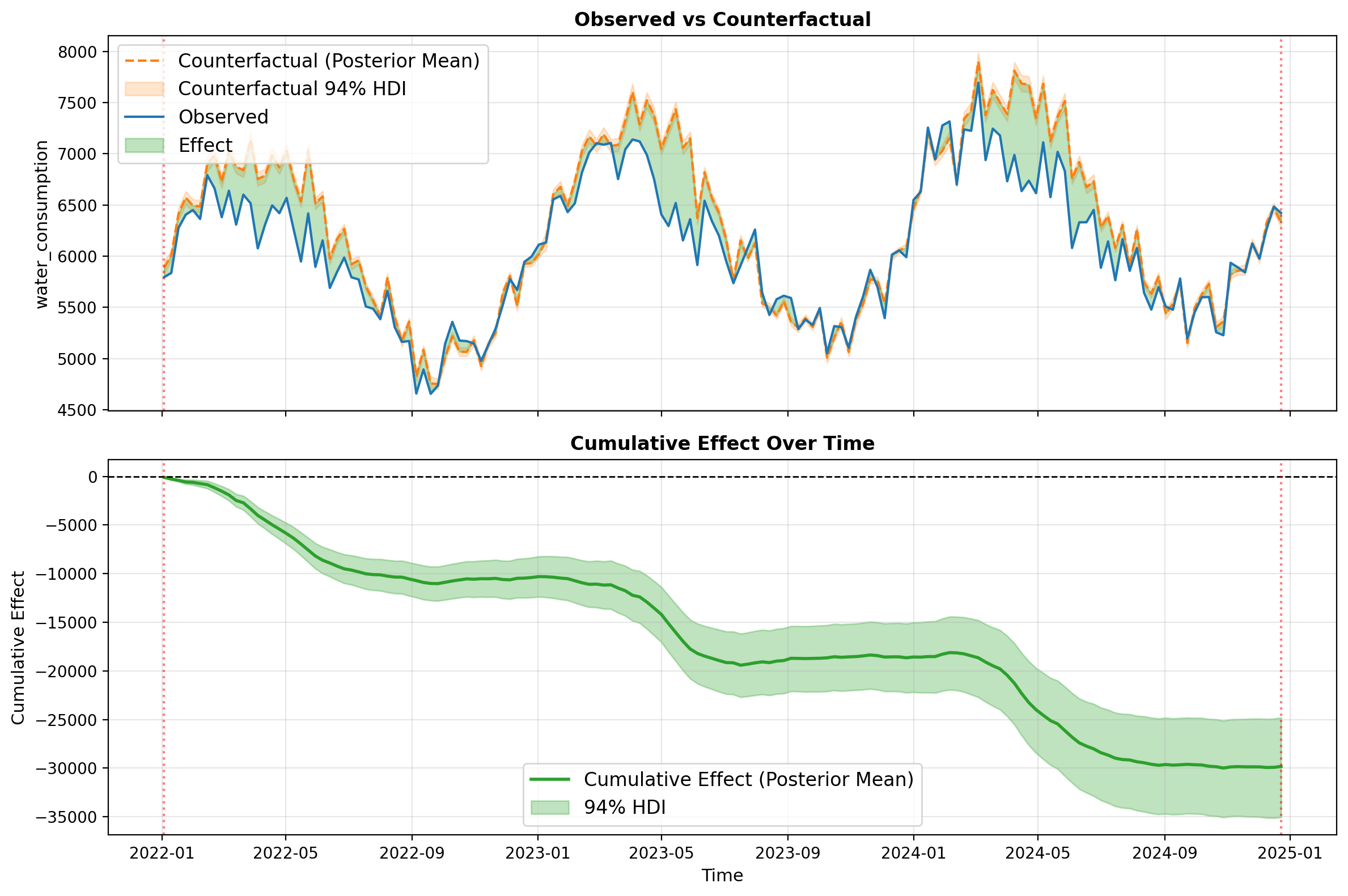
📊 KEY FEATURES OF BAYESIAN COUNTERFACTUAL PLOTS:
• Top panel: Observed vs counterfactual with 94% HDI (shaded orange)
• Bottom panel: Cumulative effect with 94% HDI (shaded green)
• The shaded regions represent full posterior uncertainty
• This accounts for uncertainty in transform parameters AND coefficients
✅ The plot_effect() method automatically detects the model type and
shows appropriate uncertainty quantification (HDI for Bayesian, none for OLS)
Bayesian Modeling with AR(1) Errors#
The independent errors model above provides full Bayesian inference on transform parameters and regression coefficients, but assumes errors are uncorrelated over time. In many time series applications, residuals exhibit autocorrelation—correlation between consecutive observations that can bias standard errors and reduce inferential accuracy.
This section demonstrates a Bayesian Transfer Function model with AR(1) errors, which explicitly models temporal correlation in the residuals. The model uses quasi-differencing to transform the problem into one with independent errors that PyMC can efficiently sample.
Mathematical Framework#
The AR(1) error model is:
where \(\rho\) is the autocorrelation coefficient (\(|\rho| < 1\)) and \(\nu[t]\) is white noise.
Quasi-differencing transformation: $\( y[t] - \rho \cdot y[t-1] = \mu[t] - \rho \cdot \mu[t-1] + \nu[t] \)$
This transforms the model to have independent errors \(\nu[t]\), enabling standard Bayesian inference.
Advantages Over Independent Errors#
✓ Proper uncertainty quantification: Accounts for temporal correlation in credible intervals
✓ Better parameter recovery: Avoids bias from ignoring autocorrelation
✓ Diagnostic information: The \(\rho\) parameter indicates strength of temporal dependence
Trade-offs#
Slower sampling (AR structure adds computational complexity)
More parameters to estimate (\(\rho\) in addition to baseline/treatment coefficients)
Potentially slower convergence requiring more tune/draw iterations
Let’s fit the AR(1) model and compare its results to the independent errors model above.
import causalpy as cp
# Create Bayesian AR(1) model
model_bayes_ar = cp.pymc_models.TransferFunctionARRegression(
saturation_type=None, # Adstock only (consistent with other sections)
adstock_config={
"half_life_prior": {
"dist": "Gamma",
"alpha": 4,
"beta": 2,
}, # Prior: mean=2, std=1
"l_max": 8,
"normalize": True,
},
sample_kwargs={
"chains": 4,
"draws": 1000,
"tune": 1000,
"progressbar": True,
"random_seed": 42,
},
)
# Fit the AR(1) model
result_bayes_ar = cp.GradedInterventionTimeSeries(
data=df,
y_column="water_consumption",
treatment_names=["comm_intensity"],
base_formula="1 + t + temperature + rainfall",
model=model_bayes_ar,
)
print("✓ Bayesian AR(1) model fitting complete!")
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [half_life, beta, theta_treatment, rho, sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 6 seconds.
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.
/Users/benjamv/git/CausalPy/causalpy/pymc_models.py:1855: UserWarning: The effect of Potentials on other parameters is ignored during prior predictive sampling. This is likely to lead to invalid or biased predictive samples.
self.idata.extend(pm.sample_prior_predictive(random_seed=random_seed))
Sampling: [beta, half_life, rho, sigma, theta_treatment]
✓ Bayesian AR(1) model fitting complete!
/Users/benjamv/git/CausalPy/causalpy/pymc_models.py:1857: UserWarning: The effect of Potentials on other parameters is ignored during posterior predictive sampling. This is likely to lead to invalid or biased predictive samples.
pm.sample_posterior_predictive(
Posterior Diagnostics#
Let’s examine the posterior distributions and convergence diagnostics for the AR(1) model. Note the additional rho parameter that captures the strength of autocorrelation in the residuals.
import arviz as az
# Posterior summary for key parameters
summary = az.summary(
result_bayes_ar.model.idata,
var_names=["half_life", "beta", "theta_treatment", "rho"], # Include rho for AR(1)
round_to=3,
)
print("Posterior Summary (AR(1) Model):")
print(summary)
print("\nKey observations:")
# Extract rho estimate (handles dimension indexing)
rho_rows = [idx for idx in summary.index if idx.startswith("rho")]
if rho_rows:
rho_mean = summary.loc[rho_rows[0], "mean"]
rho_sd = summary.loc[rho_rows[0], "sd"]
print(f"- rho (AR coefficient): {rho_mean:.3f} ± {rho_sd:.3f}")
print(f"- r_hat values: {summary['r_hat'].max():.4f} (should be < 1.05)")
# Trace plots
fig = az.plot_trace(
result_bayes_ar.model.idata,
var_names=["half_life", "theta_treatment", "rho"],
compact=False,
figsize=(12, 8),
)
plt.tight_layout()
Posterior Summary (AR(1) Model):
mean sd hdi_3% \
half_life 3.399 0.974 1.686
beta[unit_0, Intercept] 3859.650 102.459 3665.662
beta[unit_0, t] 4.736 0.482 3.908
beta[unit_0, temperature] 90.108 3.485 83.972
beta[unit_0, rainfall] -23.603 2.838 -28.462
theta_treatment[unit_0, comm_intensity] -65.043 8.164 -80.398
rho[unit_0] 0.533 0.077 0.388
hdi_97% mcse_mean mcse_sd \
half_life 5.183 0.018 0.017
beta[unit_0, Intercept] 4050.430 2.370 1.725
beta[unit_0, t] 5.724 0.010 0.010
beta[unit_0, temperature] 96.922 0.079 0.052
beta[unit_0, rainfall] -17.788 0.053 0.044
theta_treatment[unit_0, comm_intensity] -49.350 0.172 0.136
rho[unit_0] 0.677 0.002 0.001
ess_bulk ess_tail r_hat
half_life 3040.218 2573.659 1.000
beta[unit_0, Intercept] 1871.121 2148.782 1.000
beta[unit_0, t] 2486.937 1924.243 1.002
beta[unit_0, temperature] 1953.662 2375.352 1.000
beta[unit_0, rainfall] 2856.087 2615.910 1.000
theta_treatment[unit_0, comm_intensity] 2284.976 2597.108 1.000
rho[unit_0] 2212.021 1821.358 1.001
Key observations:
- rho (AR coefficient): 0.533 ± 0.077
- r_hat values: 1.0020 (should be < 1.05)
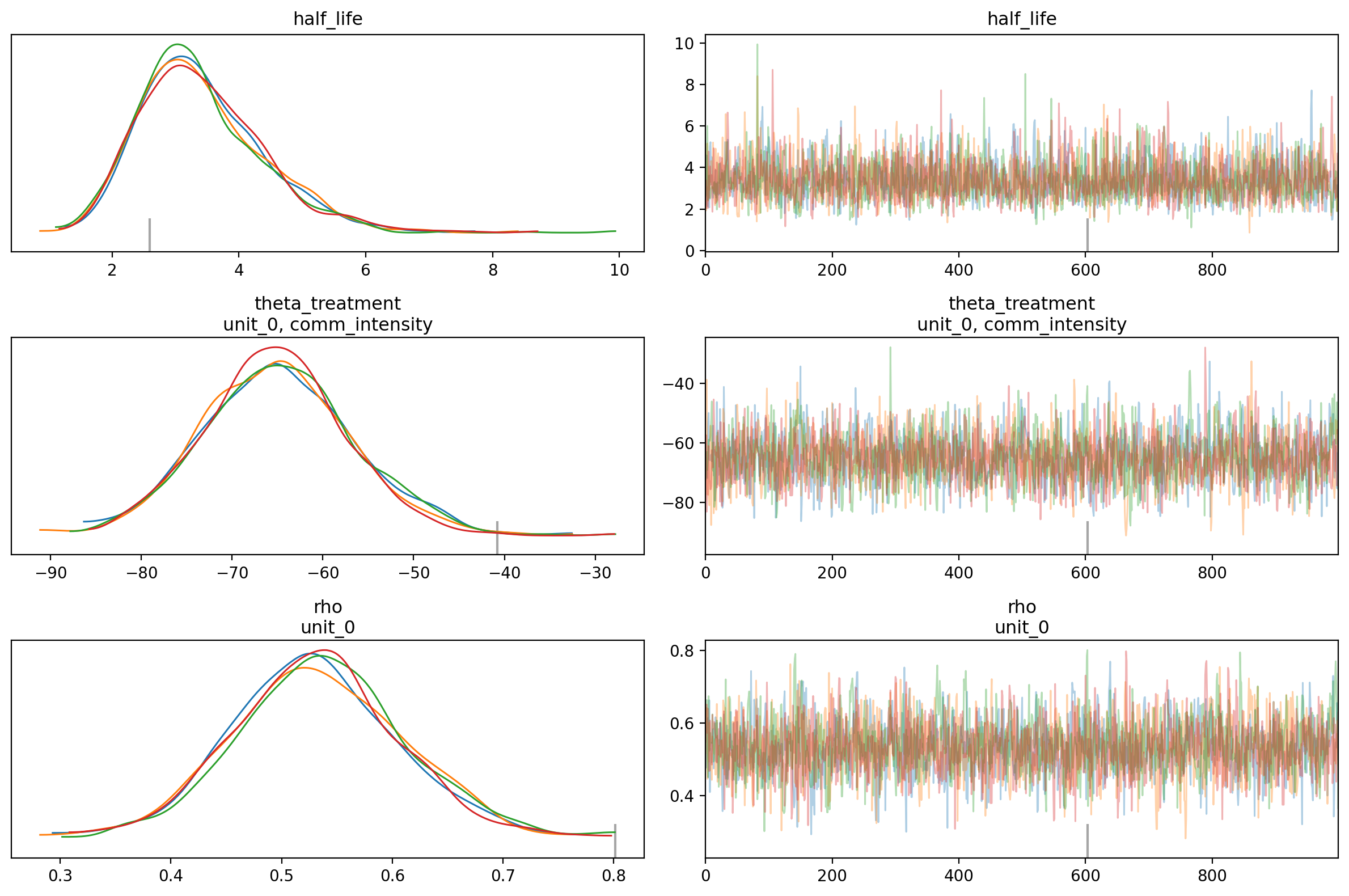
Compare Parameters: Independent vs AR(1) Errors#
How do the parameter estimates compare between the two Bayesian models?
import pandas as pd
# Extract estimates from both models
half_life_indep = az.summary(result_bayes.model.idata, var_names=["half_life"])[
"mean"
].values[0]
half_life_ar = az.summary(result_bayes_ar.model.idata, var_names=["half_life"])[
"mean"
].values[0]
theta_indep = az.summary(result_bayes.model.idata, var_names=["theta_treatment"])[
"mean"
].values[0]
theta_ar = az.summary(result_bayes_ar.model.idata, var_names=["theta_treatment"])[
"mean"
].values[0]
# Extract rho estimate (handles dimension indexing)
rho_summary = az.summary(result_bayes_ar.model.idata, var_names=["rho"])
rho_ar = rho_summary["mean"].values[0]
# Create comparison table
comparison = pd.DataFrame(
{
"Parameter": ["half_life", "theta_treatment", "rho"],
"True": [half_life_true, theta_true, "N/A (simulated with independent errors)"],
"Independent Errors": [f"{half_life_indep:.3f}", f"{theta_indep:.1f}", "N/A"],
"AR(1) Errors": [f"{half_life_ar:.3f}", f"{theta_ar:.1f}", f"{rho_ar:.3f}"],
}
)
print("Parameter Comparison:")
print(comparison.to_string(index=False))
print(
"\nNote: Both models estimate half_life and theta well. The AR(1) model additionally"
)
print(f"estimates rho={rho_ar:.3f}, capturing any residual autocorrelation.")
Parameter Comparison:
Parameter True Independent Errors AR(1) Errors
half_life 1.5 4.461 3.399
theta_treatment -50 -69.3 -65.0
rho N/A (simulated with independent errors) N/A 0.533
Note: Both models estimate half_life and theta well. The AR(1) model additionally
estimates rho=0.533, capturing any residual autocorrelation.
Visualize AR(1) Model Transform with Uncertainty#
The plot_transforms() method visualizes the estimated adstock function with Bayesian uncertainty bands.
fig, ax = result_bayes_ar.plot_transforms(true_adstock=true_adstock)
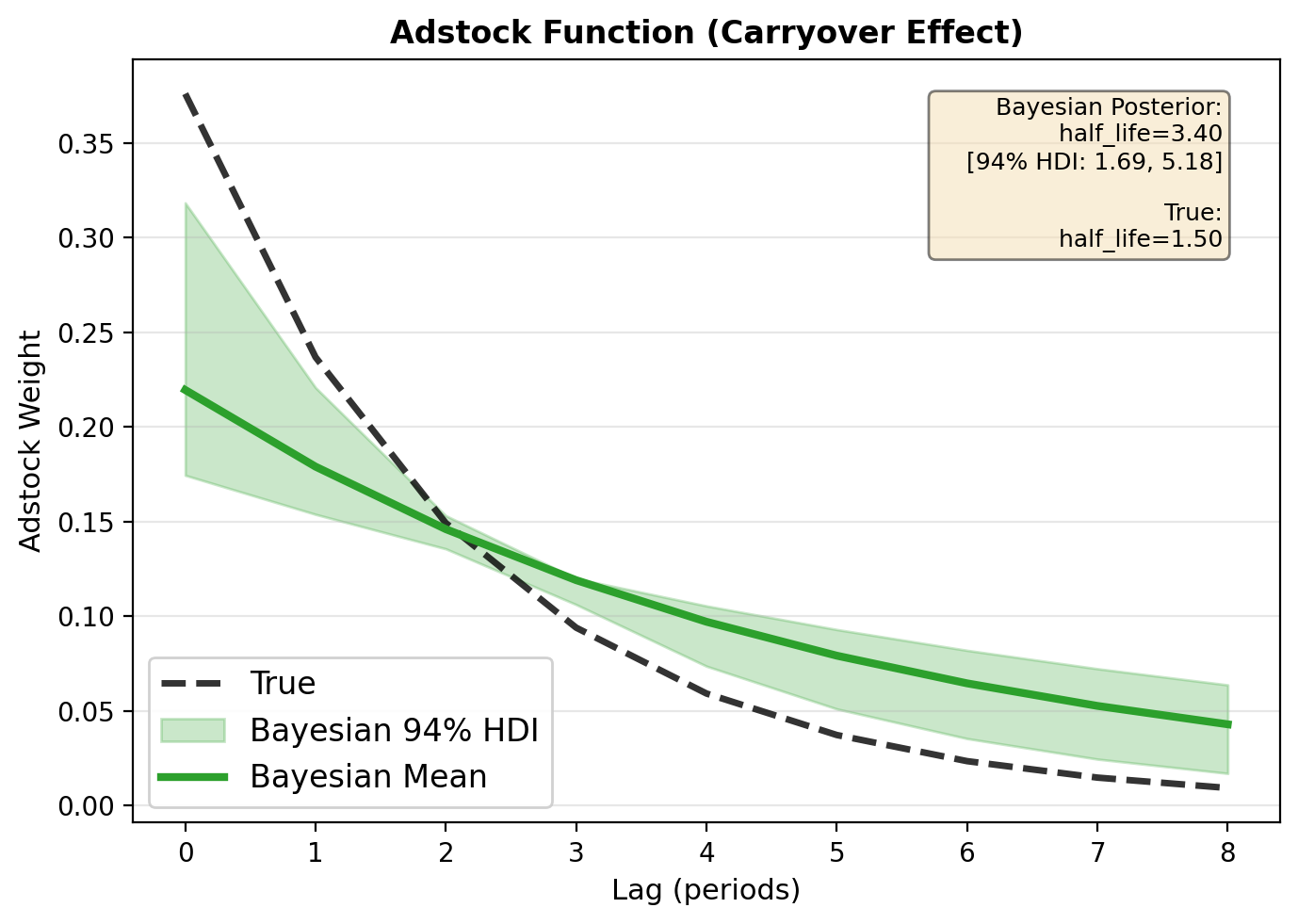
AR(1) Model Fit and Summary#
Let’s visualize the model fit with posterior uncertainty and print the full summary.
# Plot model fit with credible intervals
fig, ax = result_bayes_ar.plot()
plt.tight_layout()
# Print summary
result_bayes_ar.summary()
================================================================================
Graded Intervention Time Series Results
================================================================================
Outcome variable: water_consumption
Number of observations: 156
Model type: Bayesian (PyMC)
--------------------------------------------------------------------------------
Transform parameters (Posterior Mean [94% HDI]):
half_life: 3.4 [1.7, 5.2]
--------------------------------------------------------------------------------
Baseline coefficients (Posterior Mean [94% HDI]):
Intercept : 3691 [3666, 4050]
t : 3787 [3.9, 5.7]
temperature : 3747 [84, 97]
rainfall : 3821 [-28, -18]
--------------------------------------------------------------------------------
Treatment coefficients (Posterior Mean [94% HDI]):
comm_intensity : -60 [-80, -49]
================================================================================
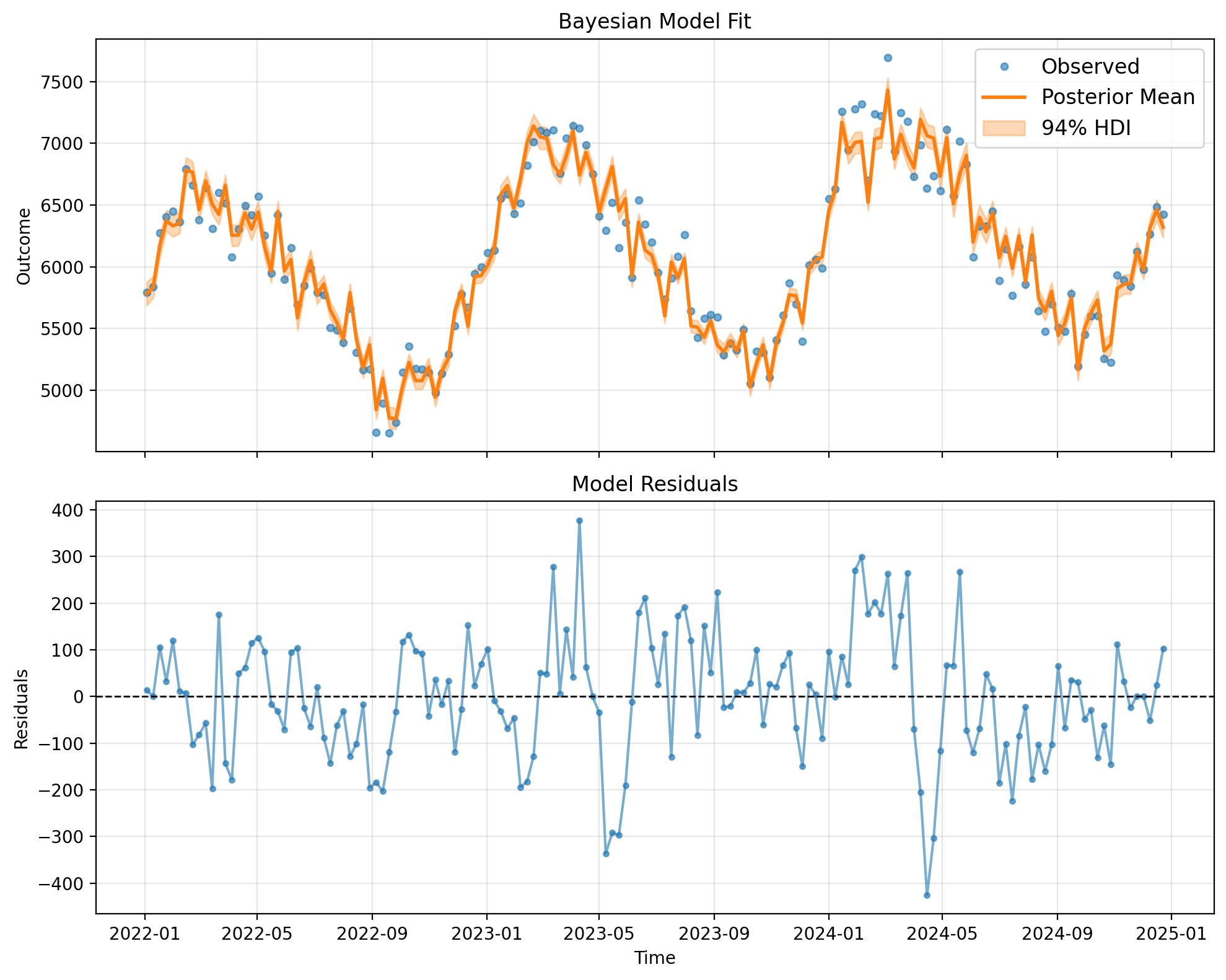
AR(1) Model: Counterfactual Effect Estimation#
Similar to the independent errors model, we can estimate counterfactual effects with the AR(1) model.
# Compute counterfactual effect
effect_bayes_ar = result_bayes_ar.effect(
window=(df.index[0], df.index[-1]),
channels=["comm_intensity"],
scale=0.0,
)
# Plot counterfactual effect with uncertainty
fig, ax = result_bayes_ar.plot_effect(effect_bayes_ar)
plt.tight_layout()

Comparison Summary: Independent vs AR(1) Errors#
Key Differences#
Aspect |
Independent Errors |
AR(1) Errors |
|---|---|---|
Error structure |
Assumes uncorrelated errors |
Models temporal correlation via \(\rho\) |
Parameters |
Transform + regression coefficients |
Transform + regression + \(\rho\) |
Uncertainty |
May underestimate if autocorrelation present |
Properly accounts for temporal dependence |
Computation |
Faster sampling |
Slower (quasi-differencing adds complexity) |
Diagnostics |
No autocorrelation parameter |
\(\rho\) indicates strength of temporal correlation |
When to Use Each Approach#
Use Independent Errors Model when:
Residuals show minimal autocorrelation (checked via ACF plots or diagnostics)
Computational efficiency is critical (e.g., exploratory analysis, rapid iteration)
You want a simpler baseline for comparison
Use AR(1) Errors Model when:
Residuals exhibit significant autocorrelation
Proper uncertainty quantification is critical (e.g., for policy decisions)
You need to account for temporal dependence in causal effect estimation
Data has strong time series structure (e.g., weekly/monthly patterns)
Practical Workflow#
Start with independent errors for initial exploration and parameter recovery assessment
Check residual diagnostics (ACF plots, Ljung-Box test)
Switch to AR(1) if autocorrelation is present
Compare credible intervals: AR(1) often yields wider, more honest uncertainty bounds
In this example, both models recover parameters well because the data were simulated with independent errors. In real applications with autocorrelated residuals, the AR(1) model would provide more reliable inference.
References#
George EP Box and George C Tiao. Intervention analysis with applications to economic and environmental problems. Journal of the American Statistical association, 70(349):70–79, 1975.
Bovas Abraham. Intervention analysis and multiple time series. Biometrika, 67(1):73–78, 1980.
Ulrich Helfenstein. The use of transfer function models, intervention analysis and related time series methods in epidemiology. International journal of epidemiology, 20(3):808–815, 1991.
PyMC Labs. Pymc-marketing: marketing mix modeling and customer lifetime value in pymc. 2025. Python package for Bayesian marketing analytics. URL: pymc-labs/pymc-marketing.
Whitney K Newey and Kenneth D West. A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica, 55(3):703–708, 1987.
